一、单选题 (共 10 题 ),每题只有一个选项正确
1. 下列各数中, 比 1 大的数是
2. 2023 年, 河南不断迸发新能量, 粮食产量为 1324.9 亿斤; 全国首个米字形高铁路网建成, 高铁运营里程达到 2215 千米; 全年接待游客 9.95 亿人次; 国家重点实验室达到 13 家, 国家级创新平台 172 家……其中的数据 “ 1324.9 亿” 用科学记数法表示为
3. 古代中国的诸多技艺均领先世界水平, 即使到现代也依然让人叹为观止. 桻卯结构就是其中最为华丽的一种, 楎卯是在两个木构件上所采用的一种凹凸结合的连接方式. 凸出部分叫㻶(或桻宽、高分别相同, 且槥头的高度也相同, 关于它们的三视图, 下列描述正确的是
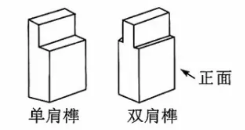
主视图相同
左视图相同
俯视图相同
三种视图都不相同
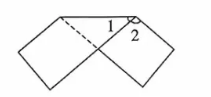
4. 在一次折纸活动中, 某小组成员将一长方形纸条折叠成如图所示的图形, 若
, 则
的度数为
5. 化简 的结果是
1
-1
6. 如果关于 的方程 有两个不相等的实数根, 则 的取值范围为
7. 如图, 点
为
上的三个点, 如果
的半径为 5 , 锐角
的正弦值为
, 则弦
的长为

3
5
6
8
8. 为落实《用好红色资源 培育时代新人 红色旅游助推铸魂育人行动计划(2023-2025 年)》, 某校积极开展红色研学精品课程建设,推动红色文化与日常教学有机融合. 目前该校已开发 “辉县人民干得好展览馆” “裴寨村” “太行红色文化教育基地” “南太行轿顶山红色抗战实物展览馆” 四个合作教育基地, 七年级(1) 班和(2)班准备从这四个基地中任选一个前往研学, 则这两个班研学地点相同的概率为
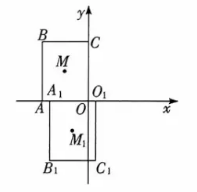
9. 在平面直角坐标系中, 规定把一个几何图形先沿着
轴翻折, 再向右平移 1 个单位长度, 这个过程为 1 次变换. 如图, 矩形
的顶点为
, 点
是矩形
的对称中心, 将矩形
进行 1 次变换之后得到矩形
, 点
的对应点为
, 则将矩形
进行 168 次变换之后, 点
的坐标为
10. 如图 1, 在平行四边形
中,
, 动点
从点
出发以
的速度沿着边
运动, 到达点
后停止运动; 同时动点
从点
出发, 以
的速度沿着边
运动, 到达点
后停止运动. 设点
的运动时间为
的面积为
, 已知
关于
的函数图象如图 2 所示, 则下列描述中错误的是
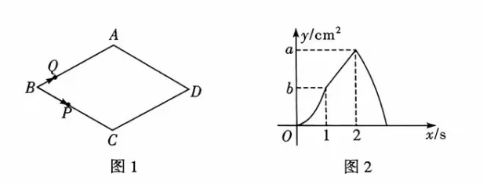
运动过程中, 的面积先增大再减小
四边形 为菱形
二、填空题 (共 5 题 ),请把答案直接填写在答题纸上
11. 2023 年 12 月 8 日, 济郑高铁全线通车, 线路全长 . 甲乘高铁从郑州前往济南, 若高铁平均行驶速度为 , 行驶 后, 甲距离济南还有 km.
12. 不等式组 的解集为
13. 种子是农业的“芯片”, 为了打好种业创新翻身仗,建设一流种业平台, 建设国家农业创新高地, 2022 年 4 月, 河南省人民政府印发《“中原农谷”建设方案》, 举全省之力在新乡打造种业创新高地. 某农科所响应号召, 大力开展对植物生长的研究, 该农科所在相同条件下进行某植物种子发芽率的试验,得到的结果如下表所示:
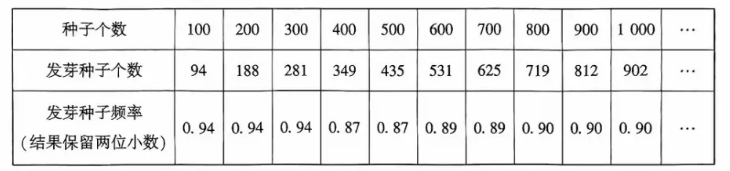
请根据以上数据, 估计 15000 个这种植物种子不发芽的约有 ________ 个
14. 如图所示的
网格中, 每个小正方形的边长均为 1 , 点
均在小正方形的顶点上, 连接
和
交于点
, 分别过点
和点
作弧形成如图所示的图案, 则图中阴影部分的面积为
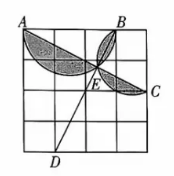
15. 在等边三角形 中, 为 内部一点, 且 为 边上一点, 且 . 当以 为顶点的三角形为直角三角形时, 的边长为
三、解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
16. (1) 计算: .
(2) 化简: .
17. 如图是由小正方形组成的
网格, 每个小正方形的顶点叫做格点, 线段
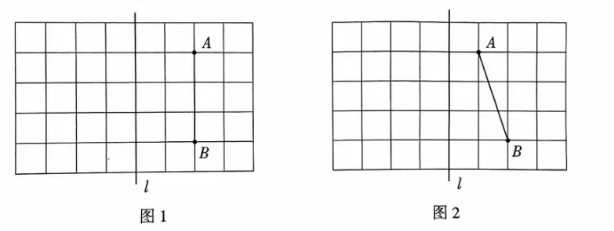
的两个端点都在格点上. 请仅用无刻度的直尺在给定网格中按下列要求完成画图.
(1) 请在图 1 和图 2 中分别作出线段
关于直线
的轴对称线段
.
(2)线段
绕某个点旋转一定的角度是否也能得到线段
? 若能, 请分别在图 1 和图 2 中作出旋转中心
; 若不能, 请说明理由 (画图过程用虚线表示).
18. 为加强劳动教育, 某校开辟了学稼园, 内设棑作区和伺养区,并把这两个区域划分为若干小块,分给七、八年级的各个班级负责. 某日,学校对各班劳动教育项目运作情况进行了一次评分, 现从七、八年级耕作区和伺养区各随机抽取 20 个项目, 并对其得分 (满分为 10 分)进行统计, 整理如下:
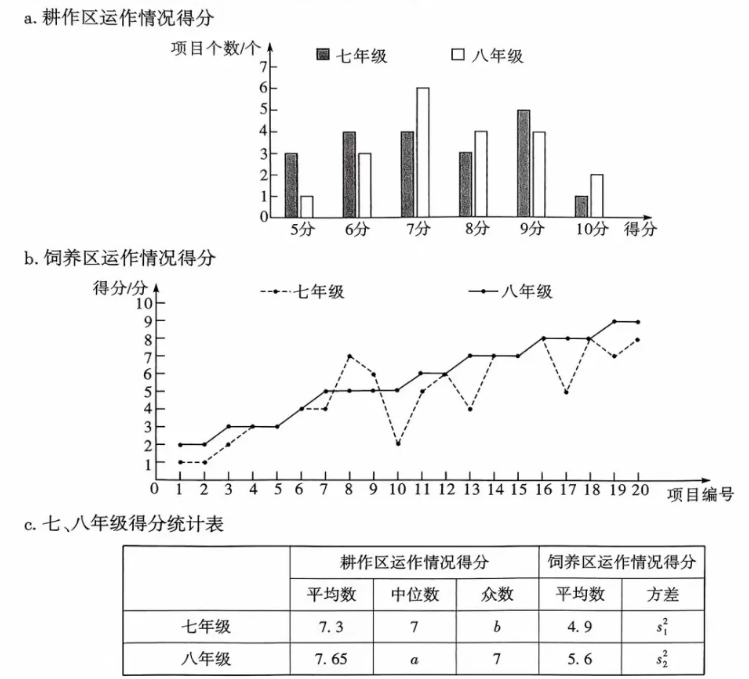
根据以上信息, 回答下列问题:
(1) 表格中
,
,
(填“>” “ < "或“ =”).
(2)该校七年级有 30 个班,八年级有 20 个班, 每班各负责 2 个耕作区项目,如果耕作区运作情况得分不低于 9 分,会被授予“示范项目”流动红旗,请你估计获得流动红旗的项目数量.
(3) 根据以上数据, 请分析哪个年级项目运作情况更好, 并说明理由.
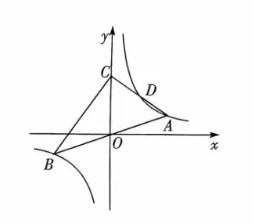
19. 如图, 反比例函数
的图象与过原点的直线交于
两点,
为
轴上一点, 连接
.
(1) 请判断
的中点
是否在该反比例函数的图象上.
(2) 在 (1) 的条件下, 连接
交
轴正半轴于点
, 求点
的坐标.
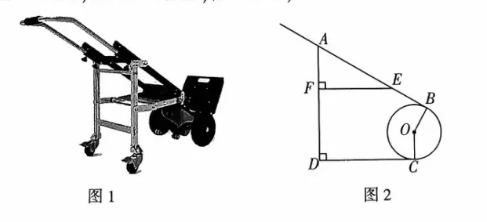
20. 爬楼机是新型的载物 (载人) 爬楼工具, 它利用本身配备的动作执行机构, 来实现上下楼动作, 进而完成上下楼的目的. 如图 1 , 这是某款爬楼机静止停放的示意图, 图 2 是该款爬楼机的侧面示意图, 车身
与轮子
相切于点
, 轮子着地点为点
地面
, 支架
在使用时可以打开并坚直支撑于地面, 打开时, 支架
与车身
夹角为
, 垂足为
. 已知
, 求该款爬楼机轮子
的直径. (结果精确到
. 参考数据:
21. 北京时间 2023 年 10 月 26 日, 神舟十七号载人飞船发射取得了圆满成功! 神舟十七号截人飞船发射成功并对接中国空间站, 标志着中国载人航天走过空间站关键技术验证阶段和建造阶段. 某商店为了满足广大航天爱好者的需求, 购进 两种飞船模型进行销售, 经了解, 该商店销售的 两种飞船模型的单价之和为 35 元, 种飞船模型的单价比 种飞船模型单价的 2 倍少 10 元.
(1)求 两种飞船模型的单价.
(2)该商店为了促销让利, 给出了两种优惠方案, 购买时只能选择其中一种方案.
方案一: 所有飞船模型打八折销售;
方案二:全场购物每满 100 元立减 25 元现金(不足 100 元不减).
(1)若购买 15 个 种飞船模型和 10 个 种飞船模型, 则选择哪一种方案更省钱? 并说明理由.
(2)若购买 种飞船模型和 B 种飞船模型共 25 个,其中 种飞船模型不少于 2 个, 当选择方案一购买时, 本次购买最少花费 元, 请直接写出 的值.
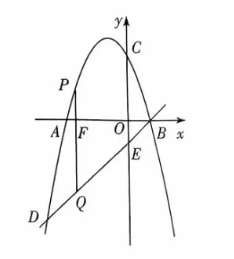
22. 如图, 抛物线
交
轴于
两点, 交
轴于点
, 直线
经过
两点,点
在抛物线上.
(1)求抛物线的解析式.
(2) 点
为直线
上方抛物线上一个动点 (不与点
重合), 过点
作
轴于点
, 交直线
于点
.
(1)求
的最大值;
(2)记抛物线上点
与点
之间的部分 (包含端点) 为图象
, 当图象
对应函数的最大值与最小值的差为 1 时, 请直接写出点
的横坐标
的取值范围.
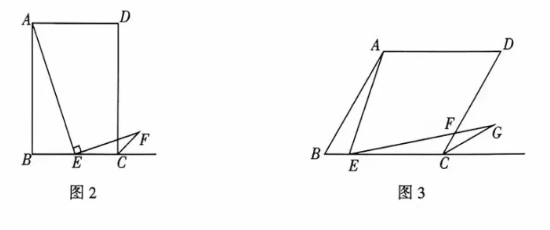
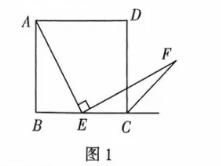
23. (1)【唤醒经历】
如图 1, 四边形
是正方形, 点
是边
的中点,
, 且
交正方形外角的平分线
于点
, 求证:
. (提示: 取
的中点
, 连接
)
上述为人教版数学教材八年级下册第 69 页第 14 题, 题中给出了问题的解决方法. 如果正方形
的边长为 4 , 则
的长为
(2)【应用经历】
如图 2, 四边形
是矩形,
, 点
是边
的中点,
, 且
交矩形的外角平分线
于点
, 求
的长.
(3)【发展经历】
如图 3, 四边形
是边长为 4 的菱形, 且
, 点
为边
上一动点, 点
为边
上一点, 且满足
所在直线与
相邻外角平分线所在直线交于点
. 若
, 请直接写出
的长.