(1)【唤醒经历】
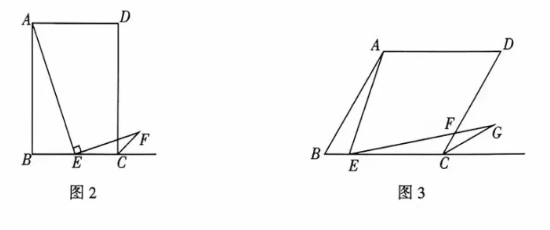
如图 1, 四边形 $A B C D$ 是正方形, 点 $E$ 是边 $B C$ 的中点, $\angle A E F=90^{\circ}$, 且 $E F$ 交正方形外角的平分线 $C F$ 于点 $F$, 求证: $A E=E F$. (提示: 取 $A B$ 的中点 $G$, 连接 $E G$ )

上述为人教版数学教材八年级下册第 69 页第 14 题, 题中给出了问题的解决方法. 如果正方形 $A B C D$ 的边长为 4 , 则 $C F$ 的长为 $\qquad$

(2)【应用经历】
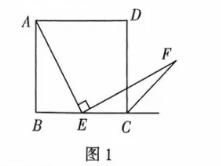
如图 2, 四边形 $A B C D$ 是矩形, $A B=6, B C=4$, 点 $E$ 是边 $B C$ 的中点, $\angle A E F=90^{\circ}$, 且 $E F$ 交矩形的外角平分线 $C F$ 于点 $F$, 求 $C F$ 的长.

(3)【发展经历】
如图 3, 四边形 $A B C D$ 是边长为 4 的菱形, 且 $\angle B=60^{\circ}$, 点 $E$ 为边 $B C$ 上一动点, 点 $F$ 为边 $C D$上一点, 且满足 $\angle A E F=60^{\circ}, E F$ 所在直线与 $\angle B C D$ 相邻外角平分线所在直线交于点 $G$. 若 $C G=2$, 请直接写出 $B E$ 的长.