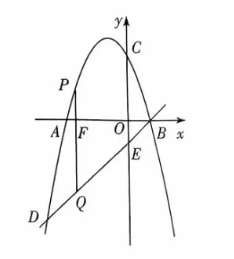
如图, 抛物线 $y=a x^2+b x+3$ 交 $x$ 轴于 $A, B(1,0)$ 两点, 交 $y$ 轴于点 $C$, 直线 $y=m x+n$ 经过 $B, D(-4,-5)$ 两点,点 $D$ 在抛物线上.
(1)求抛物线的解析式.
(2) 点 $P$ 为直线 $B D$ 上方抛物线上一个动点 (不与点 $B, D$ 重合), 过点 $P$ 作 $P F \perp x$ 轴于点 $F$, 交直线 $B D$ 于点 $Q$.
(1)求 $P Q$ 的最大值;
(2)记抛物线上点 $C$ 与点 $P$ 之间的部分 (包含端点) 为图象 $G$, 当图象 $G$ 对应函数的最大值与最小值的差为 1 时, 请直接写出点 $P$ 的横坐标 $x_P$ 的取值范围.
(1)求抛物线的解析式.
(2) 点 $P$ 为直线 $B D$ 上方抛物线上一个动点 (不与点 $B, D$ 重合), 过点 $P$ 作 $P F \perp x$ 轴于点 $F$, 交直线 $B D$ 于点 $Q$.
(1)求 $P Q$ 的最大值;
(2)记抛物线上点 $C$ 与点 $P$ 之间的部分 (包含端点) 为图象 $G$, 当图象 $G$ 对应函数的最大值与最小值的差为 1 时, 请直接写出点 $P$ 的横坐标 $x_P$ 的取值范围.
