一、单选题 (共 9 题 ),每题只有一个选项正确
1. 8的相反数是
-8
8
2. 下列事件中, 必然事件是
甲在罚球线上投篮一次, 投中
经过有交通信号灯的路口, 遇到红灯
任意画一个三角形, 其内角和是
掷一枚正方体骰子, 朝上一面的点数小于 7
3. 利用“分形”与“迭代”可以制作出很多精美的图形, 以下是制作出的几个简单图形, 其中是轴对称但不是中心对称的图形是
4. 计算 的结果是
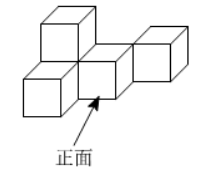
5. 如图所示的几何体的俯视图是
6. 已知点 和 都在反比例函数 的图象上, 如果 , 那么 与 的大小关系是
无法判断
7. 如图所示的游泳池内蓄满了水, 现打开深水区底部的出水口匀速放水, 在这个过程中, 可以近似地刻画出泳池水面高度
与放水时间
之间的变化情况的是

8. 为庆祝五四青年节, 志远中学举办乒乓球比赛活动, 九 (4) 班有三名男生、两名女生参加比赛, 那么从这五名学生中任选两人, 正好组成一男一女的混合双打的概率是
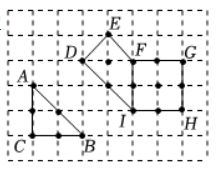
9. 在边长为 1 的小正方形组成的方格纸中, 称小正方形的顶点为 “格点”, 顶点全在格点上的多边形为 “格点多边形”. 格点多边形的面积记为
, 其内部的格点数记为
, 边界上的格点数记为
, 例如, 图中的
是格点三角形, 其中
; 图中格点多边形
所对应的
分别是
. 经探究发现, 任意格点多边形的面积
可表示为
, 其中
为常数, 则当
时,
的值为
44
43
100
99
二、填空题 (共 6 题 ),请把答案直接填写在答题纸上
11. 某班为了解学生每周“家务劳动”情况, 随机调查了7名学生每周的劳动时间, 一周内累计参加家务劳动的时间分别为: 2 小时, 3 小时, 2 小时, 3 小时, 2.5 小时, 3 小时, 1.5 小时, 则这组数据的中位数为 ________ 小时.
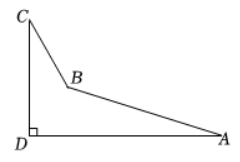
13. 如图, 小明去爬山, 在坡比为
的山坡
上走
, 此时小明看山顶
的仰角为 6
, 则山高
为
( 结果保留根号) .
14. 已知抛物线 是常数, , 且 . 下列四个结论: (1)若 , 则抛物线经过点 ;(2)抛物线与 轴一定有两个不同的公共点;(3)一元二次方程 有一个根 ; (4)点 、 在抛物线上, 若当 时, 总有 , 则 . 其中正确的是 ( 填写序号 ) 。
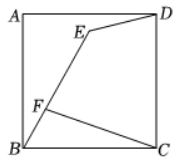
15. 如图, 在边长为 6 的正方形
中, 将
绕点
逆时针旋转
得到
是
上一点, 且
, 连接
, 则
的最小值为
三、解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
16. 解不等式组 , 请按下列步骤完成解答.
( 1 ) 解不等式(1), 得
( 2 ) 解不等式(2), 得
(3)把不等式(1)和(2)的解集在数轴上表示出来.
17. 如图
分别平分
, 交
于点
.
(1) 求证:
;
(2) 若
, 求
的度数.
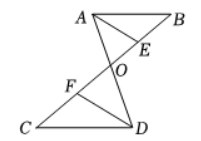
18. 2022 年某市居民人均消费支出构成情况如下面的图表所示.
请根据其中的信息回答以下问题:
(1)2022年该市居民人均总支出为元, 图 2 中其他支出所对应扇形的圆心角的度数为
(2) 请将图1补充完整.
( 3 ) 小明家 2022 年人均消费总支出为 3 万元, 请你估计小明家 2022 年的人均饮食支出约为多少元?
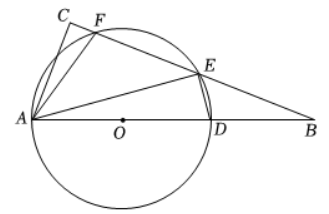
19. 19. (8分) 如图, 在
中,
为
边上一点, 以点
为圆心,
为半径作
, 与
相交于
两点, 与
交于点
, 连接
.
(1) 求证:
;
(2) 若
为
弧的中点, 求
的值.
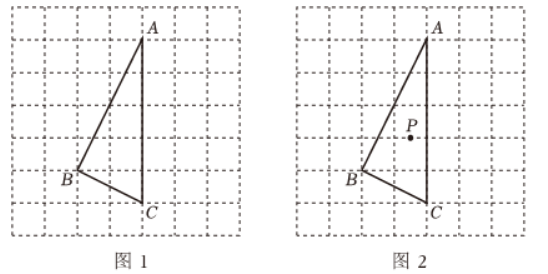
20. 如图是由小正方形组成的
网格, 每个小正方形的顶点叫做格点,
的三个顶点都是格点,
是网格线上的一点. 仅用无刻度的直尺在给定网格中完成画图, 画图过程用虚线表示.
(1) 在图1中, 先画出
的角平分线
, 再在
上画点
, 使
;
(2) 在图 2 中, 先画出点
关于直线
的对称点
, 再画
, 使
.
21. 行驶中的汽车刹车后, 由于惯性还会继续向前滑行一段距离, 这段距离称为 “刹车距离”. 已知汽车 刹车后刹车距离 (单位: ) 与刹车时的速度 (单位: ) 的函数关系满足 . 当汽车的速度为 时, 刹车距离为 ;当汽车的速度为 时, 刹车距离为 .
(1) 求 关于 的函数解析式;
( 2 ) 行驶中的汽车 突然发现正前方 处有一辆抛针的危险用品运输车, 紧急刹车, 此时汽车 的速度为 , 通过计算判断汽车 是否会撞上运输车;
(3) 若汽车 刹车后刹车距离 (单位: ) 与刹车时的速度 (单位: ) 的函数关系满足 , 当 时, 在相同的车速下汽车 的“刹车距离”始终比汽车 的“刹车距离”大, 直接写出 的取值范围.
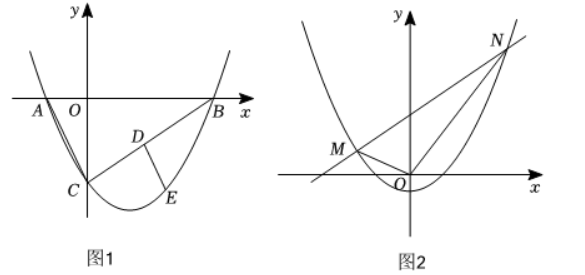
22. 如图1, 在
中,
是
延长线上一点,
, 连接
是
延长线上一点,
.
问题提出: 当
时, 探究
的值.
(1) 先将问题特殊化. 如图 2 , 当
时, 直接写出
的值;
(2)再将问题一般化. 如图1, 证明(1)中的结论仍成立;
问题拓展:
(3) 如图 3 , 过点
作
于点
, 若
, 直接写出
的值 (用含
的式子表示).
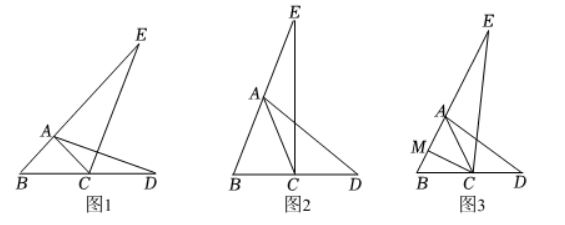
23. 如图1, 抛物线
与
轴负半轴交于点
, 与
轴正半轴交于点
, 与
轴交于点
, 且
2 .
(1) 求
的值;
( 2 )
为第四象限抛物线上一点,
交
于点
. 若
, 求点
的坐标;
( 3 ) 如图 2 , 平移抛物线
得到抛物线
, 使其顶点为
, 直线
交抛物线
于
两点. 若
,求
的值.