如图1, 抛物线 $C_1: y=\frac{1}{3} x^2+b x-4$ 与 $x$ 轴负半轴交于点 $A$, 与 $x$ 轴正半轴交于点 $B$, 与 $y$ 轴交于点 $C$, 且 $\tan \angle C A B=$ 2 .
(1) 求 $b$ 的值;

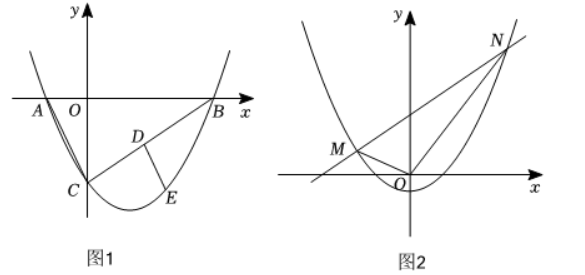
( 2 ) $E$ 为第四象限抛物线上一点, $E D / / A C$ 交 $B C$ 于点 $D$. 若 $D E=\frac{1}{2} A C$, 求点 $E$ 的坐标；
( 3 ) 如图 2 , 平移抛物线 $C_1$ 得到抛物线 $C_2$, 使其顶点为 $\left(0,-\frac{3}{4}\right)$, 直线 $y=\frac{2}{3} x+m$ 交抛物线 $C_2$ 于 $M, N$ 两点. 若 $O M+O N=9$,求 $m$ 的值.