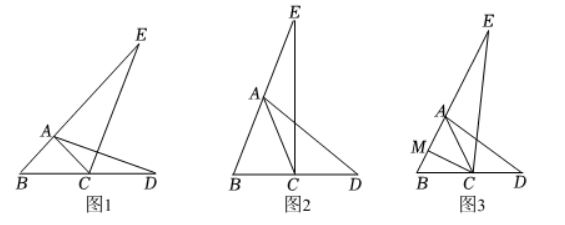
如图1, 在 $\triangle A B C$ 中, $A B=A C, D$ 是 $B C$ 延长线上一点, $C D=n B C\left(n>\frac{2}{5}\right)$, 连接 $A D, E$ 是 $B A$ 延长线上一点, $\angle E=$ $\angle D A C$.
问题提出: 当 $n=1$ 时, 探究 $\frac{A D}{C E}$ 的值.
(1) 先将问题特殊化. 如图 2 , 当 $\angle A B C=60^{\circ}$ 时, 直接写出 $\frac{A D}{C E}$ 的值;
（2）再将问题一般化. 如图1, 证明（1）中的结论仍成立；
问题拓展:
(3) 如图 3 , 过点 $C$ 作 $C M \perp B E$ 于点 $M$, 若 $\frac{A E}{A B}=\frac{3}{2}$, 直接写出 $\frac{B M}{B E}$ 的值 (用含 $n$ 的式子表示).