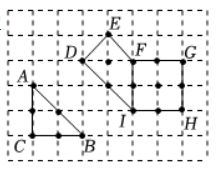
在边长为 1 的小正方形组成的方格纸中, 称小正方形的顶点为 “格点”, 顶点全在格点上的多边形为 “格点多边形”. 格点多边形的面积记为 $S$, 其内部的格点数记为 $N$, 边界上的格点数记为 $L$, 例如, 图中的 $\triangle A B C$ 是格点三角形, 其中 $S=2, N=0, L=6$; 图中格点多边形 $D E F G H I$ 所对应的 $S, N, L$ 分别是 $S$ $=7, N=3, L=10$. 经探究发现, 任意格点多边形的面积 $S$ 可表示为 $S=a N+b L+c$, 其中 $a, b, c$ 为常数, 则当 $N=82, L=38$ 时, $S$ 的值为

A. 44
B. 43
C. 100
D. 99