2024年中考数学压轴题系列

导出试卷

2024年中考数学压轴题系列

解答题（共 5 题），解答过程应写出必要的文字说明、证明过程或演算步骤

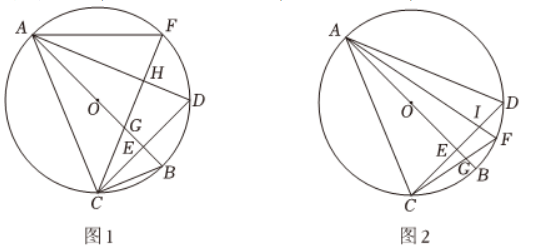
如图, 点 $C$ 在以 $A B$ 为直径的 $\odot O$ 上. 将 $\odot O$ 沿直径 $A B$ 对折, 点 $C$ 落在 $\odot O$ 上的点 $D$ 处, 分别连接 $A C, C D, A D, A$ $B$ 与 $C D$ 交于点 $E$. 另有一动点 $F$ 在 $\overparen{A D}$ 上运动, 连接 $C F$ 交 $A B$ 于点 $G$, 交 $A D$ 于点 $H$.
（1）当 $C F$ 平分 $\angle A C D$ 时.
①连结 $B C$, 求证: $B C=B G$.
②若 $E G=E B$, 求 $\frac{C G}{A D}$ 的值.
（2）当 $C F \perp A D$ 时, 探究线段 $A F$ 与 $O E$ 的长度关系.
（3）如图2, 若点 $F$ 运动到 $\overparen{C B D}$ 上, $A F$ 交 $C D$ 于点 $I$, 求证: $A C^2-A I^2=C I \cdot D I$.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图所示, 在平面直角坐标系中, 函数 $y=-2 x+b$ 与 $y=\frac{k}{x}$ 的图象相交于 $P, Q$ 两点, 已知点 $P$ 的坐标为 $(1,4)$.
（1）求函数 $y=-2 x+b$ 与 $y=\frac{k}{x}$ 的解析式；
（2）求点 $Q$ 的坐标;
（3）求 $\triangle O P Q$ 的面积.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 抛物线与 $x$ 轴交于 $A\left(x_1, 0\right), B\left(x_2, 0\right)$ 两点, 且 $x_1>x_2$, 与 $y$ 轴交于点 $C(0,4)$, 其中 $x_1, x_2$ 是方程 $x^2-2 x-8=0$ 的两个根.
（1）求这条抛物线的解析式；
（2）点 $P$ 是线段 $A B$ 上的动点, 过点 $P$ 作 $P E \| A C$, 交 $B C$ 于点 $E$, 连接 $C P$, 当 $\triangle C P E$ 的面积最大时, 求点 $P$ 的坐标;
(3) 探究: 若点 $Q$ 是抛物线对称轴上的点, 是否存在这样的点 $Q$, 使 $\triangle Q B C$ 成为等腰三角形?若存在, 请直接写出所有符合条件的点 $Q$ 的坐标; 若不存在, 请说明理由.

查看分享编辑下载此题点赞(0) 收藏(1) 错题本(1) 白板加入试卷

如图, 已知抛物线 $y=a x^2+b x+2(a < 0)$ 与 $y$ 轴交于点 $C$, 与 $x$ 轴交于 $A(-1,0), B(2,0)$ 两点.
(1) 求抛物线的函数表达式；
(2) 若点 $D$ 是第二象限抛物线上的动点, $D E \| x$ 轴, 交直线 $B C$ 于点 $E$, 点 $G$ 在 $x$ 轴上, 点 $F$ 在坐标平面内. 是否存在点 $D$, 使以 $D, E, F, G$ 为顶点的四边形是正方形? 若存在, 求点 $D$ 的坐标; 若不存在, 请说明理由.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

已知抛物线 $y=-x^2+b x+c$ 与 $x$ 轴交于 $A(-1,0), B(3,0)$ 两点, 与 $y$ 轴交于点 $C$.
(1)求拋物线的解析式;
(2)如图 1, 抛物线的对称轴交 $x$ 轴于点 $M$, 连接 $B C 、 C M$. 求 $V B C M$ 的周长及 $\tan \angle B C M$ 的值;
(3)如图 2, 过点 $A$ 的直线 $m / / B C$, 点 $P$ 是直线 $B C$ 上方抛物线上一动点, 过点 $P$ 作 $P D \perp m$, 垂足为点 $D$,连接 $B D, C D, C P, P B$. 当四边形 $B D C P$ 的面积最大时, 求点 $P$ 的坐标及四边形 $B D C P$ 面积的最大值.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。