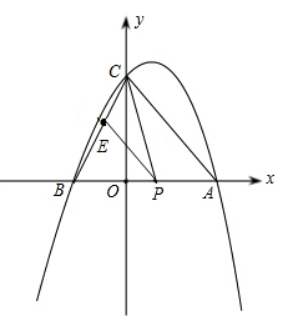
如图, 抛物线与 $x$ 轴交于 $A\left(x_1, 0\right), B\left(x_2, 0\right)$ 两点, 且 $x_1>x_2$, 与 $y$ 轴交于点 $C(0,4)$, 其中 $x_1, x_2$ 是方程 $x^2-2 x-8=0$ 的两个根.
（1）求这条抛物线的解析式；
（2）点 $P$ 是线段 $A B$ 上的动点, 过点 $P$ 作 $P E \| A C$, 交 $B C$ 于点 $E$, 连接 $C P$, 当 $\triangle C P E$ 的面积最大时, 求点 $P$ 的坐标;
(3) 探究: 若点 $Q$ 是抛物线对称轴上的点, 是否存在这样的点 $Q$, 使 $\triangle Q B C$ 成为等腰三角形?若存在, 请直接写出所有符合条件的点 $Q$ 的坐标; 若不存在, 请说明理由.