浙江省金华市 2023 年中考数学试卷

导出试卷

浙江省金华市 2023 年中考数学试卷

一、单选题（共 10 题），每题只有一个选项正确

1. 某一天, 哈尔滨、北京、杭州、金华四个城市的最低气温分别是

- 20^{\circ} C, - 10^{\circ} C, 0^{\circ} C, 2^{\circ} C

, 其中最低气温是

A.

- 20^{\circ} C

B.

- 10^{\circ} C

C.

0^{\circ} C

D.

2^{\circ} C

查看分享下载此题点赞(0) 收藏(1) 错题本(1) 白板加入试卷

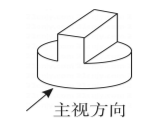
2. 某物体如图所示, 其俯视图是

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 在 2023 年金华市政府工作报告中提到, 2022 年全市共引进大学生约 123000 人, 其中数 123000 用科学记数法表示为

A.

1.23 \times 10^{3}

B.

123 \times 10^{3}

C.

12.3 \times 10^{4}

D.

1.23 \times 10^{5}

查看分享下载此题点赞(0) 收藏(1) 错题本(1) 白板加入试卷

4. 在下列长度的四条线段中, 能与长

6 cm, 8 cm

的两条线段围成一个三角形的是

A.

1 cm

B.

2 cm

C.

13 cm

D.

14 cm

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 要使

\sqrt{x - 2}

有意义, 则

x

的值可以是

A.

B.

-1

C.

-2

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 上周双休日, 某班 8 名同学课外阅读的时间如下 (单位: 时)：1, 4, 2, 4, 3, 3, 4, 5 . 这组数据的众数是

A.

1 时

B.

2时

C.

3 时

D.

4 时

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 如图, 已知

∠ 1 = ∠ 2 = ∠ 3 = 50^{\circ}

, 则

∠ 4

的度数是

A.

120^{\circ}

B.

125^{\circ}

C.

130^{\circ}

D.

135^{\circ}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

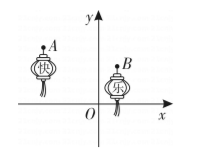
8. 如图, 两盘灯笼的位置 A, B 的坐标分别是

(- 3, 3), (1, 2)

, 将点 B 向右平移 2 个单位, 再向上平移 1 个单位得到点

B^{'}

, 则关于点

A^{'}, B^{'}

的位置描述正确是

A.

关于

x

轴对称

B.

关于

y

轴对称

C.

关于原点

O

对称

D.

关于直线

y = x

对称

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

9. 如图, 一次函数

y = a x + b

的图象与反比例函数

y = \frac{k^{2}}{}

的图象交于点

A (2, 3), B (m, - 2)

, 则不等式

a x +

b > \frac{k}{x}

的解是

A.

- 3 < x < 0

或

x > 2

B.

x < - 3

或

0 < x < 2

C.

- 2 < x < 0

或

x > 2

D.

- 3 < x < 0

或

x > 3

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 如图, 在 Rt

△ A B C

中,

∠ A C B = 90^{\circ}

, 以其三边为边在

AB

的同侧作三个正方形, 点

F

在

GH

上,

CG

与

EF

交于点

P, CM

与

BE

交于点

Q

. 若

H F = F G

, 则西四边形

P C Q E

的值是

A.

\frac{1}{4}

B.

\frac{1}{5}

C.

\frac{\sqrt{3}}{12}

D.

\frac{6}{25}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、填空题（共 6 题），请把答案直接填写在答题纸上

11. 因式分解:

x^{2} + x =

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

12. 如图, 把两根钢条

OA, OB

的一个端点连在一起, 点

C, D

分别是

OA, OB

的中点. 若

CD = 4 cm

, 则该工件内槽宽

AB

的长为

cm

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

13. 下表为某中学统计的七年级 500 名学生体重达标情况（单位：人), 在该年级随机抽取一名学生, 该生体重“标准”的概率是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

14. 在直角坐标系中, 点

(4, 5)

绕原点

O

逆时针方向旋转

90^{\circ}

, 得到的点的坐标是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

15. 如图, 在

△ ABC

中,

AB = AC = 6 cm, ∠ BAC = 50^{\circ}

, 以

AB

为直径作半圆, 交

BC

于点

D

, 交

AC

于点

E

,则弧 DE 的长为

cm

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 如图是一块矩形菜地

ABCD, AB = a (m), AD = b (m)

, 面积为

s (m^{2})

. 现将边

AB

增加

1 m

.
(1) 如图 1, 若

a = 5

, 边

AD

减少

1 m

, 得到的矩形面积不变, 则

b

的值是

(2) 如图 2, 若边

AD

增加

2 m

, 有且只有一个

a

的值, 使得到的矩形面积为

2 s (m^{2})

, 则

s

的值是

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、解答题（共 8 题），解答过程应写出必要的文字说明、证明过程或演算步骤

17. 计算:

(- 2023)^{0} + \sqrt{4} - 2 \sin 30^{\circ} + | - 5 |

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 已知

x = \frac{1}{3}

, 求

(2 x + 1) (2 x - 1) + x (3 - 4 x)

的值.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

19. 为激发学生参与劳动的兴趣, 某校开设了以“端午”为主题的活动课程, 要求每位学生在“折纸龙”“采艾叶”“做香囊” 与“包粽子”四门课程中选且只选其中一门, 随机调查了本校部分学生的选课情况, 绘制了两幅不完整的统计图. 请根据图表信息回答下列问题:

(1) 求本次被调查的学生人数, 并补全条形统计图.
(2) 本校共有 1000 名学生, 若每间教室最多可安排 30 名学生, 试估计开设 “折纸龙” 课程的教室至少需要几间.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

20. 如图, 点

A

在第一象限内,

⊙ A

与

x

轴相切于点

B

, 与

y

轴相交于点

C

, D. 连结

AB

, 过点

A

作

A H ⊥ C D

于点

H

. (1) 求证: 四边形

A B O H

为矩形. (2) 已知

⊙ A

的半径为

4, O B = \sqrt{7}

, 求弦

C D

的长.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

21. 如图, 为制作角度尺, 将长为 10 , 宽为 4 的矩形

OABC

分割成

4 \times 10

的小正方形网格.在该矩形边上取点

P

,来表示

∠ POA

的度数. 阅读以下作图过程, 并回答下列问题:

(1) 分别求点

P_{3}, P_{4}

表示的度数.
(2) 用直尺和圆规在该矩形的边上作点

P_{5}

, 使该点表示

{37.5}^{\circ}

(保留作图痕迹, 不写作法).

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

22. 兄妹俩放学后沿图 1 中的马路从学校出发, 到书吧看书后回家.哥哥步行先出发, 途中速度保持不变: 妹妹骑车, 到书吧前的速度为 200 米/分. 图 2 中的图象分别表示两人离学校的路程

s

(米) 与哥哥离开学校的时间

t

(分) 的函数关系.

(1) 求哥哥步行的速度.
(2) 已知妹妹比哥哥迟 2 分钟到书吧.
①求图中

a

的值;
②妹妹在书吧待了 10 分钟后回家, 速度是哥哥的 1.6 倍, 能否在哥哥到家前追上哥哥? 若能, 求追上时兄妹俩离家还有多远; 若不能, 说明理由.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

23. 问题：如何设计“倍力桥”的结构？
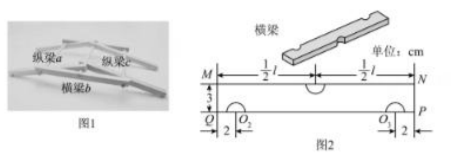
图 1 是搭成的“倍力桥”, 纵梁

a, c

夹住横梁

b

, 使得横梁不能移动, 结构稳固.
图 2 是长为

l (cm)

, 宽为

3 cm

的横梁侧面示意图, 三个凹槽都是半径为

1 cm

的半圆. 圆心分别为

O_{1}, O_{2}, O_{3}, O_{1} M = O_{1} N, O_{2} Q = O_{3} P = 2 cm

, 纵梁是底面半径为

1 cm

的圆柱体.用相同规格的横梁、纵梁搭“桥”, 间隙忽略不计.

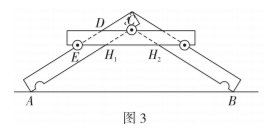
探究 1: 图 3 是“桥”侧面示意图,

A, B

为横梁与地面的交点,

C, E

为圆心,

D, H_{1}, H_{2}

是横梁侧面两边的交点. 测得

AB = 32 cm

, 点

C

到

AB

的距离为

12 cm

. 试判断四边形

{CDEH}_{1}

的形状, 并求

l

的值.

探究 2: 若搭成的“桥”刚好能绕成环, 其侧面示意图的内部形成一个多边形.
①若有 12 根横梁绕成环, 图 4 是其侧面示意图, 内部形成十二边形

H_{1} H_{2} H_{3} \dots H_{12}

, 求

l

的值;

②若有

n

根横梁绕成的环 (

n

为偶数, 且

n \geq 6

), 试用关于

n

的代数式表示内部形成的多边形

H_{1} H_{2} H_{3} \dots H_{n}

的周长.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

24. 如图, 直线

y = \frac{\sqrt{5}}{2} x + \sqrt{5}

与

x

轴,

y

轴分别交于点

A, B

, 抛物线的顶点

P

在直线

AB

上, 与

x

轴的交点为

C, D

, 其中点

C

的坐标为

(2, 0)

. 直线

BC

与直线 PD 相交于点

E

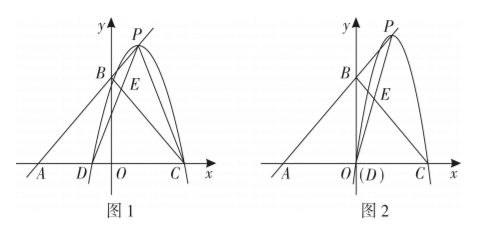
(1) 如图 2, 若抛物线经过原点

O

.
①求该抛物线的函数表达式;
②求

\frac{B E}{E C}

的值.
(2) 连结

P C, ∠ C P E

与

∠ B A O

能否相等? 若能, 求符合条件的点

P

的横坐标; 若不能, 试说明理由.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。