数学试题讲解

查看原题

如图, 直线

y = \frac{\sqrt{5}}{2} x + \sqrt{5}

与

x

轴,

y

轴分别交于点

A, B

, 抛物线的顶点

P

在直线

AB

上, 与

x

轴的交点为

C, D

, 其中点

C

的坐标为

(2, 0)

. 直线

BC

与直线 PD 相交于点

E

.

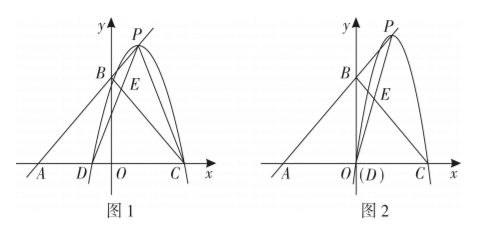
(1) 如图 2, 若抛物线经过原点

O

.
①求该抛物线的函数表达式;
②求

\frac{B E}{E C}

的值.
(2) 连结

P C, ∠ C P E

与

∠ B A O

能否相等? 若能, 求符合条件的点

P

的横坐标; 若不能, 试说明理由.