单选题 (共 12 题 ),每题只有一个选项正确
-3 的绝对值是
$\text{A.}$ -3
$\text{B.}$ 3
$\text{C.}$ $-\frac{1}{3}$
$\text{D.}$ $\frac{1}{3}$
服饰文化是我国传统文化的重要组成部分. 下列传统服饰图纹是轴对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
2023 年 2 月 28 日国家统计局发布数据显示, 2022 年我国人均国内生产总值约为 86000 元.数据 86000 用科学记数法表示为
$\text{A.}$ $86 \times 10^3$
$\text{B.}$ $8.6 \times 10^4$
$\text{C.}$ $8.6 \times 10^5$
$\text{D.}$ $0.86 \times 10^5$
已知点 $A$ 的坐标是 $(1,2)$, 那么它关于原点对称的点 $A^{\prime}$ 的坐标是
$\text{A.}$ $(2,1)$
$\text{B.}$ $(-1,2)$
$\text{C.}$ $(1,-2)$
$\text{D.}$ $(-1,-2)$
下列调查中, 适宜采用抽样调查的是
$\text{A.}$ 调查某批次汽车的抗撞击能力
$\text{B.}$ 企业招聘, 对应聘人员进行面试
$\text{C.}$ 神舟飞船发射前对其零件进行检查
$\text{D.}$ 选出某校九年级短跑最快的学生参加全市比赛
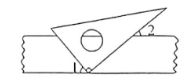
如图, 将一块三角板的顶点放在对边平行的纸条一边上. 若 $\angle 1=50^{\circ}$, 则 $\angle 2$ 的度数是
$\text{A.}$ $60^{\circ}$
$\text{B.}$ $50^{\circ}$
$\text{C.}$ $40^{\circ}$
$\text{D.}$ $30^{\circ}$
有关部门对某乒乓球生产企业一批次产品进行抽样检测, 结果如下表:

从这批产品中任取一个乒乓球, 质量检测为优等品的概率约是
$\text{A.}$ 0.97
$\text{B.}$ 0.95
$\text{C.}$ 0.94
$\text{D.}$ 0.90
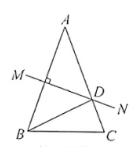
如图, $A B$ 的垂直平分线 $M N$ 交 $A C$ 于点 $D, A C=10, B C=6$, 则 $\triangle B C D$ 的周长为
$\text{A.}$ 6
$\text{B.}$ 10
$\text{C.}$ 16
$\text{D.}$ 18
下列运算正确的是
$\text{A.}$ $a^2+a^3=a^5$
$\text{B.}$ $a^8 \div a^4=a^2$
$\text{C.}$ $\left(a^3\right)^2=a^6$
$\text{D.}$ $a^2 \cdot a^2=2 a^2$
人体生命活动所需能量主要由食物中的糖类提供. 如图是小南早餐后一段时间内血糖浓度变化曲线图. 下列描述正确的是
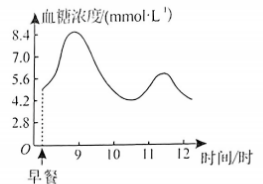
$\text{A.}$ 从 9 时至 10 时血糖呈下降状态
$\text{B.}$ 10 时血糖最高
$\text{C.}$ 从 11 时至 12 时血糖呈上升状态
$\text{D.}$ 这段时间有 3 个时刻血糖浓度达到 $7.0 \mathrm{mmol} \cdot \mathrm{L}^{-1}$
我国古代数学著作《九章算术》中记载: “今有大器五小器一容三斛, 大器一小器五容二斛. 问大小器各容几何, ”其大意为: 有大小两种盛酒的桶, 已知 5 个大桶和 1 个小桶可以盛酒 3 斛, 1 个大桶和 5 个小桶可以盛酒 2 解. 问 1 个大桶、 1 个小桶分别可以盛酒多少解? 设 1 个大桶可以盛酒 $x$ 解, 1 个小悀可以盛酒 $y$ 斛, 根据题意, 可列方程组为
$\text{A.}$ $\left\{\begin{array}{l}5 x+y=3 \\ x+5 y=2\end{array}\right.$
$\text{B.}$ $\left\{\begin{array}{l}5 x-y=3 \\ x+5 y=2\end{array}\right.$
$\text{C.}$ $\left\{\begin{array}{l}5 x+y=2 \\ x+5 y=3\end{array}\right.$
$\text{D.}$ $\left\{\begin{array}{l}x-5 y=2 \\ 5 x+y=3\end{array}\right.$
学习《设计制作长方体形状的包装纸盒》后, 小宁从长方形硬纸片上截去两个矩形 (图中阴影部分), 再沿虚线折成一个无盖的长方体纸盒.纸片长为 $30 \mathrm{~cm}$, 宽为 $18 \mathrm{~cm}, A D=2 A B$, 则该纸盒的容积为
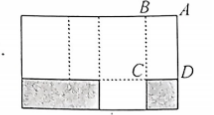
$\text{A.}$ $960 \mathrm{~cm}^3$
$\text{B.}$ $650 \mathrm{~cm}^3$
$\text{C.}$ $800 \mathrm{~cm}^3$
$\text{D.}$ $648 \mathrm{~cm}^3$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
口袋里有 7 枚除颜色外都相同的围棋子, 其中 3 枚是白色, 4 枚是黑色. 从中随机摸出一枚棋子, 颜色是黑色的概率是
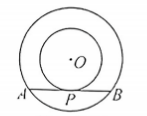
如图, 以点 $O$ 为圆心的两个同心圆中, 大圆的弦 $A B$ 是小圆的切线,点 $P$ 为切点, 大圆、小圆的半径分别为 5 和 3 , 则 $A B=$.
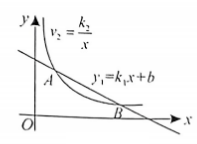
如图, 一次函数 $y_1=k_1 x+b$ 与反比例函数 $y_2=\frac{k_2}{x}(x>0)$ 的图象交于 $A(2,3), B(m, 1)$ 两点. 当 $y_1>y_2$ 时, $x$ 的取值范围是
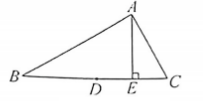
如图, 在 $\triangle A B C$ 中, $\angle C=2 \angle B$, 点 $D$ 是 $B C$ 的中点, $A E$ 是 $B C$ 边上的高. 若 $A E=2, C E=1$, 则 $D E=$.
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算: $6 \div(-3)+2^2 \times(1-4)$.
解不等式组: $\left\{\begin{array}{l}2 x+1 < 5, \text { (1) } \\ 3-x>2 . \text { (2)}\end{array}\right.$
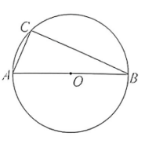
如图, $\odot O$ 是 $\triangle A B C$ 的外接圆, $A B$ 是直径.
(1) 尺规作图:作 $\angle A C B$ 的平分线交 $\odot O$ 于点 $D$;
(不写作法, 保留作图痕迹)
(2) 在 (1) 的条件下, 当 $\odot O$ 的半径为 2 时, 求 $\overparen{A D}$ 的长.
联合国教科文组织将每年的 3 月 14 日定为 “国际数学日”. 某校九年级在三月份开展了以 “数学文化” 为主题的阅读活动, 并随机抽查了部分学生在活动期间阅读相关文章的節数.
收集数据:
$$ \begin{align}
15 \quad 12 \quad18 \quad15 \quad13 \quad15 \quad 15 \quad 12 \quad 18 \quad 13 \\
18 \quad 15 \quad 13 \quad 15 \quad 12 \quad 15 \quad 13 \quad 15 \quad 18 \quad 18
\end{align}
$$
整理数据:
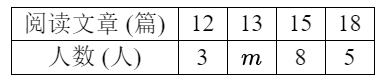
请你根据提供的信息解答下列问题:
(1) 直接写出 $m$ 的值及学生阅读篇数的中位数:
(2) 求本次调查学生阅读篇数的平均数:
(3) 若该年级大约有 300 名学生, 请你估计该校九年级学生阅读关于 “数学文化” 的文章共多少篇?
【问题情境】龙象塔位于我市肯秀山风景区, 取 “水行龙力大, 陆行象力大” 之意. 某校数学实践小组利用所学数学知识测量龙象塔的高度.
【实践探究】下面是两个方案及测量数据:
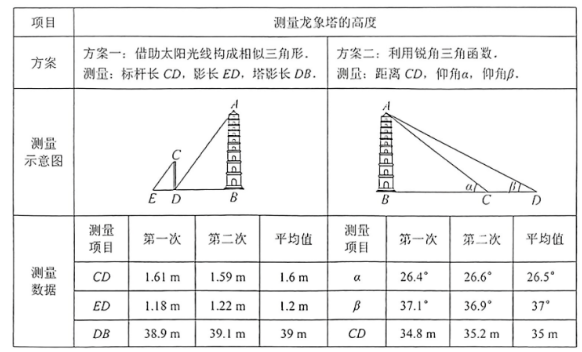
【问题解决】(1) 根据 “方案一” 的测量数据, 真接写出龙象塔 $A B$ 的高度;
(2) 根据 “方案二” 的测量数据, 求出龙象塔 $A B$ 的高度: (参考数据: $\sin 37^{\circ} \approx 0.60$, $\cos 37^{\circ} \approx 0.80, \tan 37^{\circ} \approx 0.75, \sin 26.5^{\circ} \approx 0.45, \cos 26.5^{\circ} \approx 0.89, \tan 26.5^{\circ} \approx 0.50$ )
(3)请对本次实践活动进行评价 (一条即可).
老友粉入选广西非物质文化遗产名录. 为满足消费者需求, 某超市购进甲、乙两种品牌老友粉, 已知甲品牌老友粉比乙品牌老友粉每袋进价少 2 元, 用 2700 元购进甲品牌老友粉与用 3300 元购进乙品牌老友粉的数量相同.
(1) 求甲、乙两种品牌老友粉每坺的进价:
(2)本次购进甲、乙品牌老友粉共 800 袋, 均按 13 元出售, 且购进甲品牌老友粉的数量不超过乙品牌老友粉数量的 3 倍. 若该批老友粉全部售完, 则该超市应购进甲、乙两种老友粉各多少袋才能获得最大利润? 最大利润是多少?
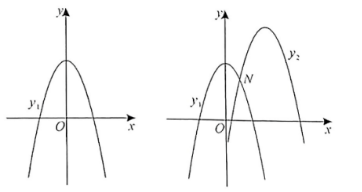
如图 1 ,抛物线 $y_1=-x^2+c$ 的图象经过 $(1,3)$.
(1) 求 $c$ 的值及抛物线 $y_1$ 的顶点坐标;
(2) 当 $-3 \leqslant x \leqslant \frac{1}{2}$ 时, 求 $y_1$ 的最大值与最小值的和;
(3) 如图 2, 将抛物线 $y_1$ 向右平移 $m$ 个单位 $(m>0)$, 再向上平移 $2 m$ 个单位得到新的抛物线 $y_2$,点 $N$ 为抛物线 $y_1$ 与 $y_2$ 的交点. 设点 $N$ 到 $x$ 轴的距离为 $n$, 求 $n$ 关于 $m$ 的函数关系式,并直接写出当 $n$ 随 $m$ 的增大而减小时, $m$ 的取值范围.
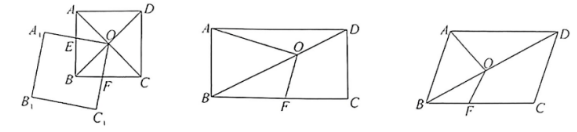
【课本再现】(1) 如图 1, 正方形 $A B C D$ 的对角线相交于点 $O$, 点 $O$ 又是正方形 $A_1 B_1 C_1 O$ 的一个顶点. 在实验与探究中, 小州发现近过证明 $\triangle B O E \cong \triangle C O F$, 可得 $O E=O F$. 请帮助小州完成证明过程:
【类比探究】(2) 如图 2, 若四边形 $A B C D$ 是矩形, $O$ 为对角线 $B D$ 上任意一点, 过 $O$ 作 $O F \perp O A$,交 $B C$ 于点 $F$, 当 $B C=2 A B$ 时, 求证: $O A=2 O F$ :
【拓展提升】(3) 如图 3, 若四边形 $A B C D$ 是平行四边形, $O$ 为对角线 $B D$ 上任意一点, 点 $F$ 在 $B C$ 上, 且 $\angle A O F=\angle B A D$, 求证: $\frac{O F}{O A}=\frac{A B}{B C}$.