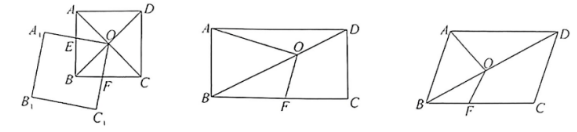
【课本再现】(1) 如图 1, 正方形 $A B C D$ 的对角线相交于点 $O$, 点 $O$ 又是正方形 $A_1 B_1 C_1 O$ 的一个顶点. 在实验与探究中, 小州发现近过证明 $\triangle B O E \cong \triangle C O F$, 可得 $O E=O F$. 请帮助小州完成证明过程:
【类比探究】(2) 如图 2, 若四边形 $A B C D$ 是矩形, $O$ 为对角线 $B D$ 上任意一点, 过 $O$ 作 $O F \perp O A$,交 $B C$ 于点 $F$, 当 $B C=2 A B$ 时, 求证: $O A=2 O F$ :
【拓展提升】(3) 如图 3, 若四边形 $A B C D$ 是平行四边形, $O$ 为对角线 $B D$ 上任意一点, 点 $F$ 在 $B C$ 上, 且 $\angle A O F=\angle B A D$, 求证: $\frac{O F}{O A}=\frac{A B}{B C}$.
【类比探究】(2) 如图 2, 若四边形 $A B C D$ 是矩形, $O$ 为对角线 $B D$ 上任意一点, 过 $O$ 作 $O F \perp O A$,交 $B C$ 于点 $F$, 当 $B C=2 A B$ 时, 求证: $O A=2 O F$ :
【拓展提升】(3) 如图 3, 若四边形 $A B C D$ 是平行四边形, $O$ 为对角线 $B D$ 上任意一点, 点 $F$ 在 $B C$ 上, 且 $\angle A O F=\angle B A D$, 求证: $\frac{O F}{O A}=\frac{A B}{B C}$.
