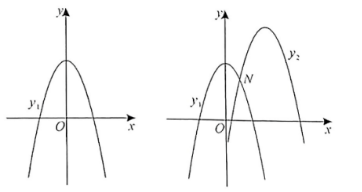
如图 1 ,抛物线 $y_1=-x^2+c$ 的图象经过 $(1,3)$.
(1) 求 $c$ 的值及抛物线 $y_1$ 的顶点坐标;
(2) 当 $-3 \leqslant x \leqslant \frac{1}{2}$ 时, 求 $y_1$ 的最大值与最小值的和;
(3) 如图 2, 将抛物线 $y_1$ 向右平移 $m$ 个单位 $(m>0)$, 再向上平移 $2 m$ 个单位得到新的抛物线 $y_2$,点 $N$ 为抛物线 $y_1$ 与 $y_2$ 的交点. 设点 $N$ 到 $x$ 轴的距离为 $n$, 求 $n$ 关于 $m$ 的函数关系式,并直接写出当 $n$ 随 $m$ 的增大而减小时, $m$ 的取值范围.