单选题 (共 14 题 ),每题只有一个选项正确
两根无限长平行直导线载有大小相等方向相反的电流 $l$, 并各以 $\mathrm{d} l / \mathrm{d} t$ 的变化率增长, 一矩形线圈位于导线平面内 $($ 如 图), 则
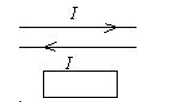
$\text{A.}$ 线圈中无感应电流.
$\text{B.}$ 线圈中感应电流为顺时针方向.
$\text{C.}$ 线圈中感应电流为逆时针方向.
$\text{D.}$ 线圈中感应电流方向不确定 .
一导体圆线圈在均匀磁场中运动,能使其中产生感应电流的一种情况是
$\text{A.}$ 线圈绕自身直径轴转动,轴与磁场方向平行
$\text{B.}$ 线圈绕自身直径轴转动,轴与磁场方向垂直
$\text{C.}$ 线圈平面垂直于磁场并沿垂直磁场方向平移
$\text{D.}$ 线圈平面平行于磁场并沿垂直磁场方向平移
如图所示,一载流螺线管的旁边有一圆形线圈,欲使线圈产生图示方向的感应电流i ,下列哪一种情况可以做到?
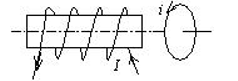
$\text{A.}$ 载流螺线管向线圈靠近
$\text{B.}$ 载流螺线管离开线圈.
$\text{C.}$ 载流螺线管中电流增大
$\text{D.}$ 载流螺线管中插入铁芯
如图所示,闭合电路由带铁芯的螺线管,电源,滑线变阻器组成.问在下列哪一种情况下可使线圈中产生的感应电动势与原电流I的方向相反

$\text{A.}$ 滑线变阻器的触点A向左滑动
$\text{B.}$ 滑线变阻器的触点A向右滑动
$\text{C.}$ 螺线管上接点B向左移动 忽略长螺线管的电阻 .
$\text{D.}$ 把铁芯从螺线管中抽出
尺寸相同的铁环与铜环所包围的面积中,通以相同变化率的磁通量,当不计环的自感时,环中
$\text{A.}$ 感应电动势不同
$\text{B.}$ 感应电动势相同,感应电流相同
$\text{C.}$ 感应电动势不同,感应电流相同
$\text{D.}$ 感应电动势相同,感应电流不同
如图, 长度为 $l$ 的直导线 $a b$ 在均匀磁场 $\vec{B}$ 中以速度 $\vec{v}$ 移动, 直导线 $a b$ 中的电动势为
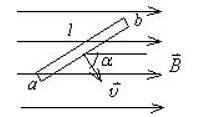
$\text{A.}$ $B l v$
$\text{B.}$ $B l \nu \sin \alpha$
$\text{C.}$ $B l v \cos \alpha$
$\text{D.}$ 0
如图所示, 直角三角形金属枉架 $a b c$ 放在均匀磁场中, 磁场 $\vec{B}$ 平行于 $a b$ 边, $b c$ 的长度为 $l$. 当金属框架绕 $a b$ 边以匀 角速度 $\omega_{\text {转动时, }} a b c$ 回路中的感应电动势 $\varepsilon_{\text {和 } \mathrm{a} 、 \mathrm{c} \text { 两点间的电势差 }} U_a-U_c$ 为
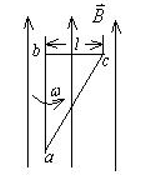
$\text{A.}$ $\varepsilon=0 \quad U_a-U_c=\frac{1}{2} B a l^2$
$\text{B.}$ $\varepsilon=0 \quad U_a-U_c=-\frac{1}{2} B a l^2$
$\text{C.}$ $\varepsilon=B a l^2 \quad U_a-U_c=\frac{1}{2} B a l^2$
$\text{D.}$ $\varepsilon=B \omega l^2 \quad U_a-U_c=-\frac{1}{2} B \omega l^2$
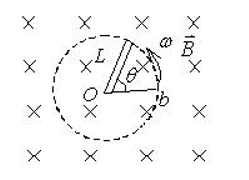
一根长度为 $L$ 的铜棒, 在均匀磁场 $\vec{B}$ 中以匀角速度 $\omega$ 绕通过其一端 $O$ 的定轴旋转着, $\vec{B}$ 的方向垂直铜棒转动的 平面,如图所示. 设 $t=0$时,铜棒与$ \mathrm{Ob} $ 成 $ \theta$角 ( $b$ 为铜棒转动的平面上的一个固定点),则在任一时刻 $t$ 这根铜棒两端 之间的感应电动势是:
$\text{A.}$ $\omega L^2 B \cos (\omega t+\theta)$
$\text{B.}$ $\frac{1}{2} \omega L^2 B \cos \omega t$
$\text{C.}$ $2 \omega L^2 B \cos (\omega t+\theta)$
$\text{D.}$ $\frac{1}{2} \omega L^2 B$
有两个线圈, 线圈 1 对线圈 2 的互感系数为 $M_{21}$, 而线圈 2 对线圈 1 的互感系数为 $M_{12}$. 若它们分别流过 ${i_1}$ 和 ${i_2}$ 的变化电流且 $\left|\frac{d i_1}{d t}\right|>\left|\frac{d i_2}{\mathrm{~d} t}\right|$, 并设由 ${i_2}$ 变化在线圈 1 中产生的互感电动势为 $\varepsilon_{12}$, 由 $i_1$ 变化在线圈 2 中产生的互感电动势为 $\varepsilon_{21}$, 判断下述哪个论断正确. ()
$\text{A.}$ $M_{12}=M_{21} \quad \varepsilon_{21}=\varepsilon_{12}$
$\text{B.}$ $M_{12} \neq M_{21} \quad \varepsilon_{21} \neq \varepsilon_{12}$
$\text{C.}$ $M_{12}=M_{21}, \varepsilon_{21}>\varepsilon_{12}$
$\text{D.}$ $M_{12}=M_{21}, \quad \varepsilon_{21} < \varepsilon_{12}$
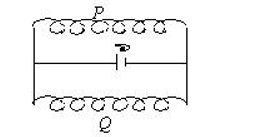
如图所示, 两个线圈 $P$ 和 $Q$ 并联地接到一电动势恒定的电源上. 线圈 $P$ 的自感和电阻分别是线圈 $Q$ 的两倍, 线圈 $P$ 和 $Q$ 之间的互感可忽略不计. 当达到稳定状态后, 线圈 $\mathrm{P}$ 的磁场能量与 $\mathrm{Q}$ 的磁场能量的比值是
$\text{A.}$ 4
$\text{B.}$ 2
$\text{C.}$ 1
$\text{D.}$ $\dfrac{1}{2}$
有两个长直密绕螺线管, 长度及线圈匝数均相同, 半径分别为 $\mathrm{r}_1$ 和 $\mathrm{r}_2$. 管内充满均匀介质, 其磁导率分别为 $\mu_1$ 和 $\mu_2$. 设 $\mathrm{r}_1: \mathrm{r}_2=1: 2, \mu_1: \mu_2=2: 1$, 当将两只螺线管串联在电路中通电稳定后, 其自感系数之比 $\mathrm{L}_1: \mathrm{L}_2$ 与磁能之比 $\mathrm{W}_{\mathrm{m1}}: \mathrm{W}_{\mathrm{m} 2}$ 分别为
$\text{A.}$ $\mathrm{L}_1: \mathrm{L}_2=1: 1, \quad \mathrm{~W}_{\mathrm{m} 1}: \mathrm{W}_{\mathrm{m} 2}=1: 1$
$\text{B.}$ $ \mathrm{~L}_1: \mathrm{L}_2=1: 2, \quad \mathrm{~W}_{\mathrm{m} 1}: \mathrm{W}_{\mathrm{m} 2}=1: 1$
$\text{C.}$ $ \mathrm{~L}_1: \mathrm{L}_2=1: 2, \quad \mathrm{~W}_{\mathrm{m} 1}: \mathrm{W}_{\mathrm{m} 2}=1: 2$
$\text{D.}$ $\mathrm{~L}_1: \mathrm{L}_2=2: 1, \quad \mathrm{~W}_{\mathrm{m} 1}: \mathrm{W}_{\mathrm{m} 2}=2: 1$
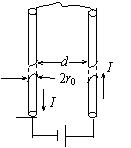
两根很长的平行直导线,其间距离 $d$ 、与电源组成回路如图 . 已知导线上的电流为 $I$, 两根导线的横截面的半径均为 $r_0$. 设用 $L$ 表示两导线回路单位长度的自感系数,则沿导线单位长度的空间内的总磁能 $W_m$ 为
$\text{A.}$ $\frac{1}{2} L I^2$.
$\text{B.}$ $\frac{1}{2} L I^2+I^2 \int_{\gamma_0}^{\infty}\left[\frac{\mu_0 I}{2 \pi r}-\frac{\mu_0 I}{2 \pi(d+r)}\right]^2 2 \pi r d r$
$\text{C.}$ $\infty$.
$\text{D.}$ $\frac{1}{2} L l^2+\frac{\mu_0 I^2}{2 \pi} \ln \frac{d}{r_0}$
真空中一根无限长直细导线上通电流 $I$, 则距导线垂直距离为 $a$ 的空间某点处的磁能密度为
$\text{A.}$ $\frac{1}{2} \mu_0\left(\frac{\mu_0 I}{2 \pi a}\right)^2$
$\text{B.}$ $\frac{1}{2 \mu_0}\left(\frac{\mu_0 I}{2 \pi a}\right)^2$
$\text{C.}$ $\frac{1}{2}\left(\frac{2 \pi a}{\mu_0 I}\right)^2$
$\text{D.}$ $\frac{1}{2 \mu_0}\left(\frac{\mu_0 I}{2 a}\right)^2$
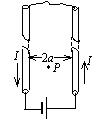
真空中两根很长的相距为2a的平行直导线与电源组成闭合回路如图.已知导线中的电流为I,则在两导线正中间某点P处的磁能密度为
$\text{A.}$ $\frac{1}{\mu_0}\left(\frac{\mu_0 I}{2 \pi a}\right)^2$.
$\text{B.}$ $\frac{1}{2 \mu_0}\left(\frac{\mu_0 I}{2 \pi a}\right)^2$.
$\text{C.}$ $\frac{1}{2 \mu_0}\left(\frac{\mu_0 I}{\pi a}\right)^2$.
$\text{D.}$ 0
填空题 (共 10 题 ),请把答案直接填写在答题纸上
用导线制成一半径为 $r=10 \mathrm{~cm}$ 的闭合圆形线圈,其电阻 $R=10 \Omega$, 均匀磁场垂直于线圈平面. 欲使电路中有一稳定的 感应电流 $i=0.01 \mathrm{~A}, B$ 的变化率应为 $\mathrm{d} B / \mathrm{d} t=$
如图所示, 一导线构成一正方形线圈然后对折,并使其平面垂直置于均匀磁场 $\bar{B}$. 当线圈的一半不动,另一半以角速度 $\omega$张开时 ( 线圈边长为 2l) , 线圈中感应电动势的大小 $\varepsilon=$
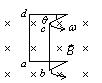
半径为 $\alpha$ 的无限长密绕螺线管, 单位长度上的匝数为 $n$ ,通以交变电流 $i= I_m \sin a t$, 则围在管外的同轴圆形回路 (半 径为 $r$ ) 上的感生电动势为
已知在一个面积为 $S$ 的平面闭合线圈的范围内,有一随时间变化的均匀磁场 $\vec{B}(t)$, 则此闭合线圈内的感应电动势 $\varepsilon_{=}$
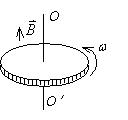
金属圆板在均匀磁场中以角速度 $\omega$ 绕中心轴旋转, 均匀磁场的方向平行于转轴, 如图所示, 这时板中由中心至同一边缘 点的不同曲线上总感应电动势的大小 ________ , 方向 ________
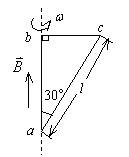
如图所示,一直角三角形 $\mathrm{abc}$ 回路放在一磁感强度为 B 的均匀磁场中, 磁场的方向与直角边 $\mathrm{ab}$ 平行, 回路绕 $\mathrm{ab}$ 边以匀角速度 $\omega$ 旋转,则 ac 边中的动生电动势为 ________ ,整个回路产生的动生电动势为 ________
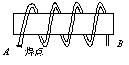
如图,两根彼此紧靠的绝缘的导线绕成一个线圈,其A端用焊锡将二根导线焊在一起,另一端B处作为连接外电路的两个输入端.则整个线圈的自感系数为
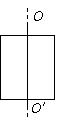
有一根无限长直导线绝缘地紧贴在矩形线圈的中心轴$OO′$上,则直导线与矩形线圈间的互感系数为
真空中两只长直螺线管 1 和 2 , 长度相等, 单层密绕匝数相同,直径之比 $d_1 / d_2=1 / 4$. 当它们通以相同电流时, 两螺线 管则存的磁能之比为 $W_1 / W_2=$
真空中一根无限长直导线中通有电流 $I$, 则距导线垂直距离为 $\mathrm{a}$ 的某点的磁能密度 ${w_m}=$
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
一面积为S的单匝平面线圈,以恒定角速度 $ \omega $ 在磁感强度 $ \vec{B}=B_0 \sin \omega t \vec{k}$ 的均匀外磁场中转动, 转轴与线圈共面且与 $\vec{B}$垂直 其中 $\vec{k}$ 为沿 $z$ 轴的单位矢量. 设 $t=0$ 时线圈的正法向与 $\vec{k}$ 同方向, 求线圈中的感应电动势.
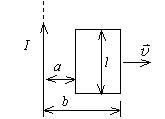
如图所示, 有一根长直导线, 载有直流电流 $I$, 近旁有一个两条对边与它平行并与它共面的矩形线圈, 以匀速度 $\vec{\nu}$ 沿垂 直于导线的方向离开导线 设 $t=0$ 时, 线圈位于图示位置, 求
(1)在任意时刻 $t^2$ 通过矩形线圈的磁通量 $\Phi$.
(2)在图示位置时矩形线圈中的电动势 $\varepsilon$.
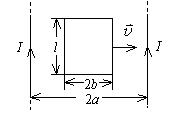
在两根平行放置相距2a的无限长直导线之间,有一与其共面的矩形线圈,线圈边长分别为l和2b,且 l边与长直导线平行.两根长直导线中通有等值同向稳恒电流I ,线圈以恒定速度$\vec{v}$ 垂直直导线向右运动 如图所示 .求:线圈运动到两导线的中心位置 即线圈的中心线与两根导线距离均为a 时,线圈中的感应电动势.
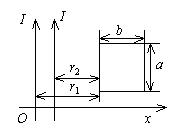
如图所示, 两条平行长直导线和一个矩形导线框共面. 且导线框的一个边与长直导线平行, 他到两长直导线的距离分别 为 $r_1 、 r_2$. 已知两导线中电流都为 $I=I_0 \sin \omega t$ ,其中 $I_0$ 和 $\omega$ 为常数, $t$ 为时间. 导线框长为 $a$ 宽为 $b$, 求导线框中的感 应电动势.
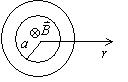
一长圆柱状磁场,磁场方向沿轴线并垂直图面向里, 磁场大小既随到轴线的距离 $r$ 成正比而变化, 又随时间 ${ }^t$ 作正弦变 化, 即 $B=B_0 r \sin \omega t, B_0 、 \omega$ 均为常数. 若在磁场内放一半径为 $a$ 的金属圆环, 环心在圆柱状磁场的轴线上, 求金 属环中的感生电动势, 并讨论其方向.
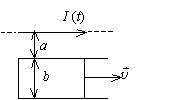
如图所示,真空中一长直导线通有电流 $I(t)=I_0 \mathrm{e}^{-\lambda t}$ (式中 $I_0 、 \lambda$为常量, $ t$为时间 ) , 有一带滑动边的矩形导线框 与长直导线平行共面,二者相距 $a$. 矩形线框的滑动边与长直导线垂直, 它的长度为 $b$, 并且以匀速 $\vec{J}$ (方向平行长直导 线) 滑动. 若忽略线框中的自感电动势,并设开始时滑动边与对边重合, 试求任意时刻 $t$ 在矩形线框内的感应电动势 $\varepsilon_i$ 并讨论 $\varepsilon_i$ 方向
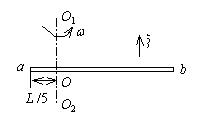
如图所示,一根长为 $L$ 的金属细杆 $a b$ 绕竖直轴 $O_1 O_2$ 以角速度 $\omega$ 在水平面内旋转. $O_1 O_2$ 在离细杆 $a$ 端 $L / 5$ 处. 若已知地 磁场在竖直方向的分量为 $\vec{B}$. 求 $a b$ 两端间的电势差 $U_a-U_b$
如图所示, 长直导线 $A B$ 中的电流 $l$ 沿导线向上, 并以 $\mathrm{d} l / \mathrm{d} t=2 \mathrm{~A} / \mathrm{s}$ 的变化率均匀增长. 导线附近放一个与之同面的直 角三角形线框,其一边与导线平行,位置及线框尺寸如图所示. 求此线框中产生的感应电动势的大小和方
向 $\left(\mu_0=4 \pi \times 10^{-7} \mathrm{~T} \cdot \mathrm{m} / \mathrm{A}\right)$
