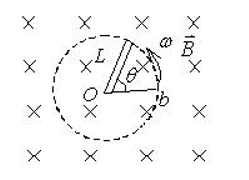
一根长度为 $L$ 的铜棒, 在均匀磁场 $\vec{B}$ 中以匀角速度 $\omega$ 绕通过其一端 $O$ 的定轴旋转着, $\vec{B}$ 的方向垂直铜棒转动的 平面,如图所示. 设 $t=0$时,铜棒与$ \mathrm{Ob} $ 成 $ \theta$角 ( $b$ 为铜棒转动的平面上的一个固定点),则在任一时刻 $t$ 这根铜棒两端 之间的感应电动势是:

A. $\omega L^2 B \cos (\omega t+\theta)$
B. $\frac{1}{2} \omega L^2 B \cos \omega t$
C. $2 \omega L^2 B \cos (\omega t+\theta)$
D. $\frac{1}{2} \omega L^2 B$