单选题 (共 10 题 ),每题只有一个选项正确
-2 的相反数是
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ 2
$\text{C.}$ -2
$\text{D.}$ $\frac{1}{2}$
若 $\angle A=40^{\circ}$ ,则 $\angle A$ 的余角的大小是
$\text{A.}$ $50^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $140^{\circ}$
$\text{D.}$ $160^{\circ}$
不等式 $3 x-2>4$ 的解集是
$\text{A.}$ $x>-2$
$\text{B.}$ $x < -2$
$\text{C.}$ $x>2$
$\text{D.}$ $x < 2$
用配方法解方程 $x^2-2 x=2$ 时,配方后正确的是
$\text{A.}$ $(x+1)^2=3$
$\text{B.}$ $(x+1)^2=6$
$\text{C.}$ $(x-1)^2=3$
$\text{D.}$ $(x-1)^2=6$
若 $\triangle A B C \sim \triangle D E F, B C=6, E F=4$ ,则 $\frac{A C}{D F}=$
$\text{A.}$ $\frac{4}{9}$
$\text{B.}$ $\frac{9}{4}$
$\text{C.}$ $\frac{2}{3}$
$\text{D.}$ $\frac{3}{2}$
2022 年 4 月 16 日,神州十三号载人飞船返回舱在东风着陆场成功着陆,飞行任务取得圆满成功."出差"太空半年的神州十三号航天员乘组顺利完成既定全部任务,并解锁了多个"首次".其中,航天员们在轨驻留期间共完成 37 项空间科学实验,如图是完成各领域科学实验项数的扇形统计图,下列说法错误的是
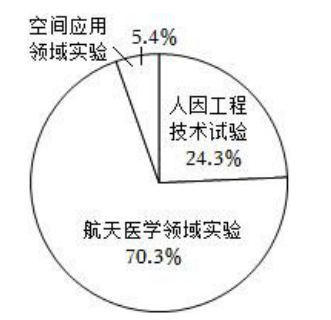
$\text{A.}$ 完成航天医学领域实验项数最多
$\text{B.}$ 完成空间应用领域实验有 5 项
$\text{C.}$ 完成人因工程技术实验项数比空间应用领域实验项数多
$\text{D.}$ 完成人因工程技术实验项数占空间科学实验总项数的 $24.3 \%$
大自然中有许多小动物都是"小数学家",如图1,蜜蜂的蜂巢结构非常精巧、实用而且节省材料,多名学者通过观测研究发现:蜂巢巢房的横截面大都是正六边形。如图2,一个巢房的横截面为正六边形 $A B C D E F$ ,若对角线 $A D$ 的长约为 8 mm ,则正六边形 $A B C D E F$ 的边长为

$\text{A.}$ 2 mm
$\text{B.}$ $2 \sqrt{2}$ mm
$\text{C.}$ $2 \sqrt{3} $ mm
$\text{D.}$ 4 mm
《九章算术》是中国古代的一部数学专著,其中记载了一道有趣的题:"今有嵬起南海,七日至北海;雁起北海,九日至南海.今癿雁俱起,问何日相逢?"大意是:今有野鸭从南海起飞, 7 天到北海;大雁从北海起飞, 9 天到南海.现野鸭从南海、大雁从北海同时起飞,问经过多少天相遇?设经过 $x$ 天相遇,根据题意可列方程为
$\text{A.}$ $\left(\frac{1}{7}+\frac{1}{9}\right) x=1$
$\text{B.}$ $\left(\frac{1}{7}-\frac{1}{9}\right) x=1$
$\text{C.}$ $(9-7) x=1$
$\text{D.}$ $(9+7) x=1$
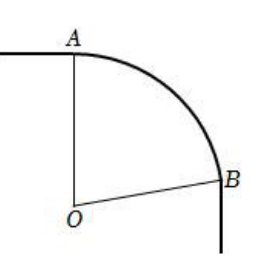
如图,一条公路(公路的宽度忽略不计)的转弯处是一段圆弧 $(\overparen{A B})$ ,点 $O$ 是这段弧所在圆的圆心,半径 $O A=90 \mathrm{~m}$ ,圆心角 $\angle A O B=80^{\circ}$ ,则这段弯路 $(\overparen{A B})$ 的长度为
$\text{A.}$ $20 \pi m$
$\text{B.}$ $30 \pi m$
$\text{C.}$ $40 \pi m$
$\text{D.}$ $50 \pi m$
如图 1,在菱形 $A B C D$ 中,$\angle A=60^{\circ}$ ,动点 $P$ 从点 $A$ 出发,沿折线 $A D \rightarrow D C \rightarrow C B$ 方向匀速运动,运动到点 $B$ 停止.设点 $P$ 的运动路程为 $x, \triangle A P B$ 的面积为 $y, y$ 与 $x$ 的函数图象如图 2所示,则 $A B$ 的长为
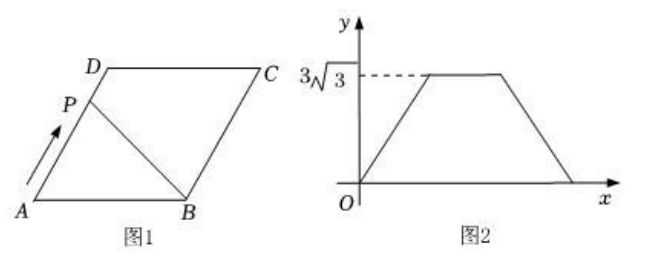
$\text{A.}$ $\sqrt{3}$
$\text{B.}$ $2 \sqrt{3}$
$\text{C.}$ $3 \sqrt{3}$
$\text{D.}$ $4 \sqrt{3}$
填空题 (共 8 题 ),请把答案直接填写在答题纸上
若一次函数 $y=k x-2$ 的函数值 $y$ 随着自变量 $x$ 值的增大而增大,则 $k=$ $\_\_\_\_$ (写出一个满足条件的值)
如图,菱形 $A B C D$ 中,对角线 $A C$ 与 $B D$ 相交于点 $O$ ,若 $A B=2 \sqrt{5} \mathrm{~cm}, A C=4 \mathrm{~cm}$ ,则 $B D$的长为 $\_\_\_\_$ cm.

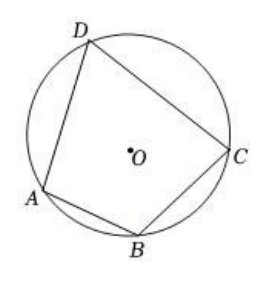
如图,$\odot$ 是四边形 $A B C D$ 的外接圆,若 $\angle A B C=110^{\circ}$ ,则 $\angle A D C=$ $\_\_\_\_$ ${ }^{\circ}$ .
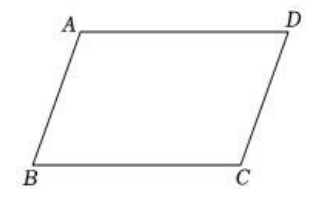
如图,在四边形 $A B C D$ 中,$A B / / D C, A D / / B C$ ,在不添加任何辅助线的前提下,要想四边形 $A B C D$ 成为一个矩形,只需添加的一个条件是
如图,以一定的速度将小球沿与地面成一定角度的方向击出时,小球的飞行路线是一条抛物线.若不考虑空气阻力,小球的飞行高度 $h$(单位:$m$ )与飞行时间 $t$(单位:$s$ )之间具有函数关系:$h=-5 t^2+20 t$ ,则当小球飞行高度达到最高时,飞行时间 $t=$ $\_\_\_\_$ $s$ .
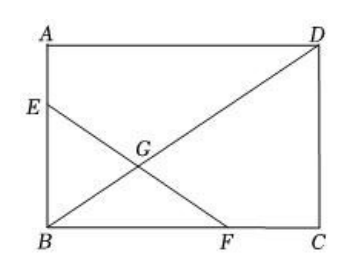
如图,在矩形 $A B C D$ 中,$A B=6 c m, B C=9 c m$ ,点 $E, F$ 分别在边 $A B, B C$ 上,$A E=2 c m$ , $B D, E F$ 交于点 $G$ ,若 $G$ 是 $E F$ 的中点,则 $B G$ 的长为 $\_\_\_\_$ cm.
解答题 (共 10 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算:$\sqrt{2} \times \sqrt{3}-\sqrt{24}$ .
化简:$\frac{(x+3)^2}{x+2} \div \frac{x^2+3 x}{x+2}-\frac{3}{x}$ .
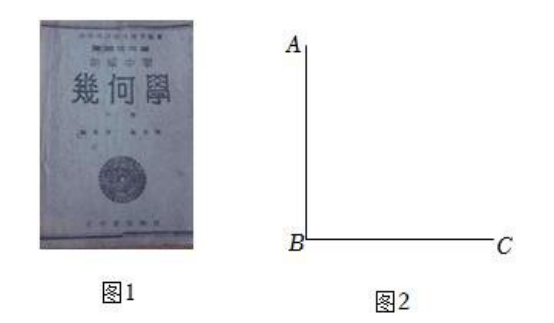
中国清朝末期的几何作图教科书《最新中学教科书用器画》由国人自编(图 1),书中记载了大量几何作图题,所有内容均用浅近的文言文表述,第一编记载了这样一道几何作图题:

(1)根据以上信息,请你用不带刻度的直尺和圆规,在图2中完成这道作图题(保留作图痕迹,不写作法);
(2)根据(1)完成的图,直接写出 $\angle D B G, \angle G B F, \angle F B E$ 的大小关系.
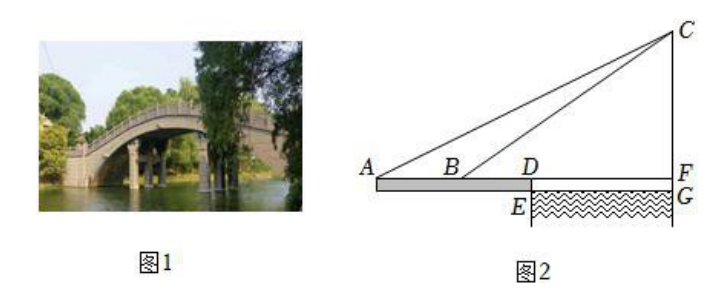
灞陵桥位于甘肃省渭源县城南清源河(渭河上游)上,始建于明洪武初年,因"渭水绕长安,绕灞陵,为玉石栏杆灞陵桥"之语,得名灞陵桥(图 1),该桥为全国独一无二的纯木质叠梁拱桥。某综合实践研究小组开展了测量汛期某天"灞陵桥拱梁顶部到水面的距离"的实践活动,过程如下:
方案设计:如图 2,点 $C$ 为桥拱梁顶部(最高点),在地面上选取 $A, B$ 两处分别测得 $\angle C A F$ 和 $\angle C B F$的度数( $A, B, D, F$ 在同一条直线上),河边 $D$ 处测得地面 $A D$ 到水面 $E G$ 的距离 $D E(C, F, G$ 在同一条直线上,$D F / / E G, C G \perp A F, F G=D E$ ).
数据收集:实地测量地面上 $A, B$ 两点的距离为 8.8 m ,地面到水面的距离 $D E=1.5 \mathrm{~m}, \angle C A F= 26.6^{\circ}, \angle C B F=35^{\circ}$ .
问题解决:求灞陵桥拱梁顶部 $C$ 到水面的距离 $C G$(结果保留一位小数).
参考数据: $\sin 26.6^{\circ} \approx 0.45, \cos 26.6^{\circ} \approx 0.89, \tan 26.6^{\circ} \approx 0.50, \sin 35^{\circ} \approx 0.57, \cos 35^{\circ} \approx 0.82$ , $\tan 35^{\circ} \approx 0.70$ .
根据上述方案及数据,请你完成求解过程.
第 24 届冬季奥林匹克运动会于 2022 年 2 月 4 至 20 日在我国北京-张家口成功举办,其中张家口赛区设有四个冬奥会竞赛场馆,分别为:A.云顶滑雪公园、B.国家跳台滑雪中心、 C.国家越野滑雪中心、D.国家冬季两项中心.小明和小颖都是志愿者,他们被随机分配到这四个竞赛场馆中的任意一个场馆的可能性相同.
(1)小明被分配到D.国家冬季两项中心场馆做志愿者的概率是多少?
(2)利用画树状图或列表的方法,求小明和小颖被分配到同一场馆做志愿者的概率.
受疫情影响,某初中学校进行在线教学的同时,要求学生积极参与"增强免疫力、丰富学习生活"为主题的居家体育锻炼活动,并实施锻炼时间目标管理.为确定一个合理的学生居家锻炼时间的完成目标,学校随机抽取了 30 名学生周累计居家锻炼时间(单位:h)的数据作为一个样本,并对这些数据进行了收集、整理和分析,过程如下:
【数据收集】
$$
\begin{aligned}
& 7 \quad 8\quad 6\quad 5\quad 9\quad 10\quad 4\quad 6\quad 7\quad 5\quad 11\quad 12\quad 8\quad 7\quad 6\quad \\
& 4\quad 6\quad 3\quad 6\quad 8\quad 9\quad 10\quad 10\quad 13\quad 6\quad 7\quad 8\quad 3\quad 5\quad 10\quad
\end{aligned}
$$
【数据整理】
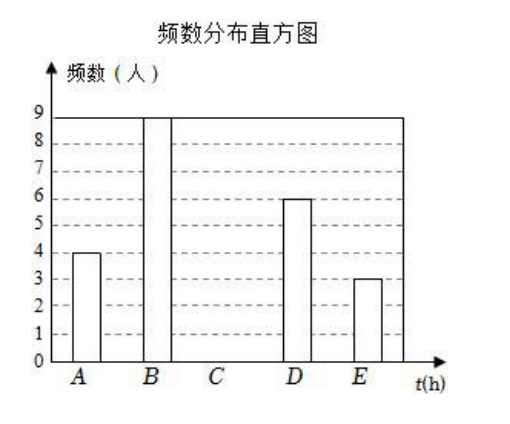
将收集的 30 个数据按 $A, B, C, D, E$ 五组进行整理统计,并绘制了如图所示的不完整的频数分布直方图(说明:$A .3 \leq t < 5, B .5 \leq t < 7, C .7 \leq t < 9, D .9 \leq t < 11, E .11 \leq t \leq 13$,其中 $t$ 表示锻炼时间);
【数据分析】

请根据以上信息解答下列问题:
(1)填空:$m=$ $\_\_\_\_$ ;
(2)补全频数分布直方图;
(3)如果学校将管理目标确定为每周不少于 $7 h$ ,该校有 600 名学生,那么估计有多少名学生能完成目标?你认为这个目标合理吗?说明理由.
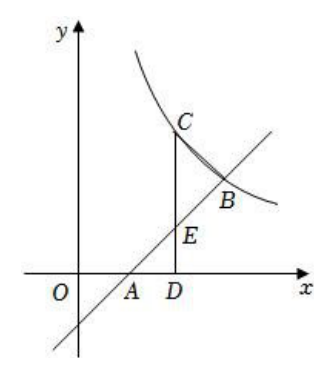
如图,$B, C$ 是反比例函数 $y=\frac{k}{x}(k \neq 0)$ 在第一象限图象上的点,过点 $B$ 的直线 $y=x-1$与 $x$ 轴交于点 $A, C D \perp x$ 轴,垂足为 $D, C D$ 与 $A B$ 交于点 $E, O A=A D, C D=3$ .
(1)求此反比例函数的表达式;
(2)求 $\triangle B C E$ 的面积.
如图,$\triangle A B C$ 内接于 $\odot O, A B, C D$ 是 $\odot O$ 的直径,$E$ 是 $D B$ 延长线上一点,且 $\angle D E C=\angle A B C$ .
(1)求证:$C E$ 是 $\odot O$ 的切线;
(2)若 $D E=4 \sqrt{5}, A C=2 B C$ ,求线段 $C E$ 的长.

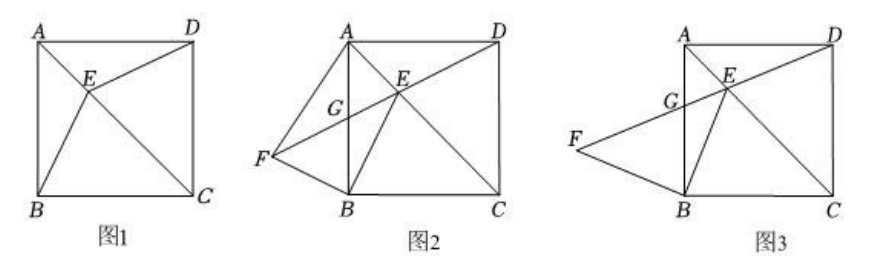
已知正方形 $A B C D, E$ 为对角线 $A C$ 上一点.
【建立模型】
(1)如图 1,连接 $B E, D E$ .求证:$B E=D E$ ;
【模型应用】
(2)如图 2,$F$ 是 $D E$ 延长线上一点,$F B \perp B E, E F$ 交 $A B$ 于点 $G$ .
① 判断 $\triangle F B G$ 的形状,并说明理由;
② 若 $G$ 为 $A B$ 的中点,且 $A B=4$ ,求 $A F$ 的长.
【模型迁移】
(3)如图 3,$F$ 是 $D E$ 延长线上一点,$F B \perp B E, E F$ 交 $A B$ 于点 $G, B E=B F$ .求证:$G E=(\sqrt{2}-1) D E$ .
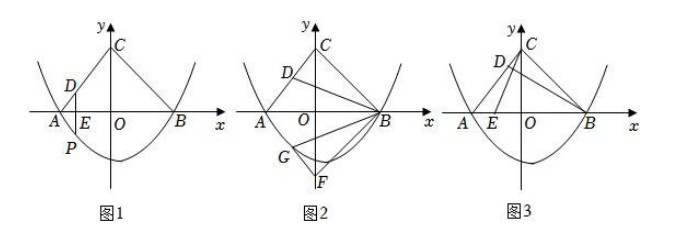
如图 1,在平面直角坐标系中,抛物线 $y=\frac{1}{4}(x+3)(x-a)$ 与 $x$ 轴交于 $A, B(4,0)$ 两点,点 $C$ 在 $y$ 轴上,且 $O C=O B, D, E$ 分别是线段 $A C, A B$ 上的动点(点 $D, E$ 不与点 $A, B, C$ 重合).
(1)求此抛物线的表达式;
(2)连接 $D E$ 并延长交抛物线于点 $P$ ,当 $D E \perp x$ 轴,且 $A E=1$ 时,求 $D P$ 的长;
(3)连接 $B D$ .
① 如图 2,将 $\triangle B C D$ 沿 $x$ 轴翻折得到 $\triangle B F G$ ,当点 $G$ 在抛物线上时,求点 $G$ 的坐标;
② 如图3,连接CE,当CD=AD时,求BD+CE的最小值