单选题 (共 8 题 ),每题只有一个选项正确
2025 年 4 月,位于我国甘肃省武威市的钍基熔盐实验堆实现连续稳定运行,标志着人类在第四代核电技术上迈出关键一步。该技术利用钍核( ${ }_{90}^{232} Th$ )俘获 $x$ 个中子( ${ }_0^1 n$ ),共发生 $y$ 次 $\beta$ 衰变,转化为易裂变的铀核( ${ }_{92}^{233} U$ ),则( )
$\text{A.}$ $x=1, y=1$
$\text{B.}$ $x=1, y=2$
$\text{C.}$ $x=2, y=1$
$\text{D.}$ $x=2, y=2$
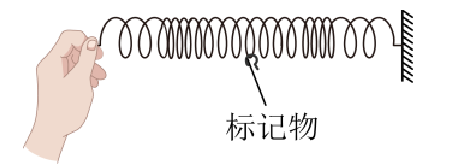
如图,某同学演示波动实验,将一根长而软的弹簧静置在光滑水平面上,弹簧上系有一个标记物,在左端沿弹簧轴线方向周期性地推、拉弹簧,形成疏密相间的机械波。下列表述正确的是( )
$\text{A.}$ 弹簧上形成的波是横波
$\text{B.}$ 推、拉弹簧的周期越小,波长越长
$\text{C.}$ 标记物振动的速度就是机械波传播的速度
$\text{D.}$ 标记物由静止开始振动的现象表明机械波能传递能量
在恒温容器内的水中,让一个导热良好的气球缓慢上升。若气球无漏气,球内气体(可视为理想气体)温度不变,则气球上升过程中,球内气体( )
$\text{A.}$ 对外做功,内能不变
$\text{B.}$ 向外放热,内能减少
$\text{C.}$ 分子的平均动能变小
$\text{D.}$ 吸收的热量等于内能的增加量
汽车由静止开始沿直线从甲站开往乙站,先做加速度大小为 $a$ 的匀加速运动,位移大小为 $x$ ;接着在 $t$ 时间内做匀速运动;最后做加速度大小也为 $a$ 的匀减速运动,到达乙站时速度恰好为 0 。已知甲、乙两站之间的距离为 $8 x$ ,则( )
$\text{A.}$ $x=\frac{1}{18} a t^2$
$\text{B.}$ $x=\frac{1}{16} a t^2$
$\text{C.}$ $x=\frac{1}{8} a t^2$
$\text{D.}$ $x=\frac{1}{2} a t^2$
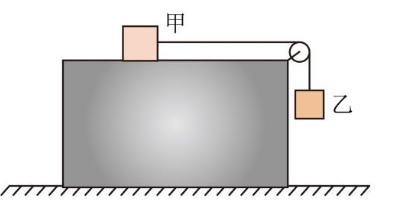
如图,装有轻质光滑定滑轮的长方体木箱静置在水平地面上,木箱上的物块甲通过不可伸长的水平轻绳绕过定滑轮与物块乙相连。乙拉着甲从静止开始运动,木箱始终保持静止。已知甲、乙质量均为 1.0 kg ,甲与木箱之间的动摩擦因数为 0.5 ,不计空气阻力,重力加速度 g 取 $10 m / s ^2$ ,则在乙下落的过程中()
$\text{A.}$ 甲对木箱的摩擦力方向向左
$\text{B.}$ 地面对木箱的支持力逐渐增大
$\text{C.}$ 甲运动的加速度大小为 $2.5 m / s ^2$
$\text{D.}$ 乙受到绳子的拉力大小为 5.0 N
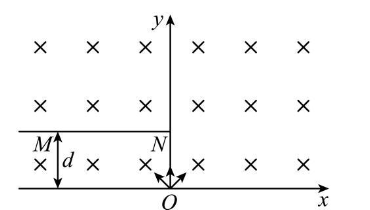
如图,在坚直平面内的 $O x y$ 直角坐标系中,$x$ 轴上方存在垂直纸面向里的匀强磁场,磁感应强度大小为 $B$ 。在第二象限内,垂直纸面且平行于 $x$ 轴放置足够长的探测薄板 $M N, M N$ 到 $x$ 轴的距离为 $d$ ,上、下表面均能接收粒子。位于原点 $O$ 的粒子源,沿 $O x y$ 平面向 $x$ 轴上方各个方向均匀发射相同的带正电粒子。已知粒子所带电荷量为 $q$ 、质量为 $m$ 、速度大小均为 $\frac{q B d}{m}$ 。不计粒子的重力、空气阻力及粒子间的相互作用,则( )
$\text{A.}$ 粒子在磁场中做圆周运动的半径为 $2 d$
$\text{B.}$ 薄板的上表面接收到粒子的区域长度为 $\sqrt{3} d$
$\text{C.}$ 薄板的下表面接收到粒子的区域长度为 $d$
$\text{D.}$ 薄板接收到的粒子在磁场中运动的最短时间为 $\frac{\pi m}{6 q B}$
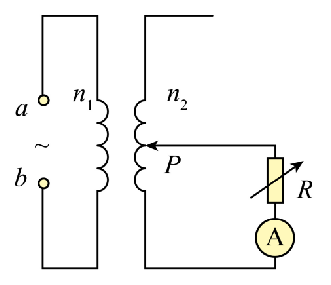
某理想变压器的实验电路如图所示,原、副线圈总匝数之比 $n_1: n_2=1: 3, A$ 为理想交流电流表。初始时,输入端 $a 、 b$ 间接入电压 $u=12 \sqrt{2} \sin (100 \pi t) V$ 的正弦式交流电,变压器的滑动触头 $P$ 位于副线圈的正中间,电阻箱 $R$ 的阻值调为 $6 \Omega$ 。要使电流表的示数变为 2.0 A ,下列操作正确的是( )
$\text{A.}$ 电阻箱 $R$ 的阻值调为 $18 \Omega$
$\text{B.}$ 副线圈接入电路的匝数调为其总匝数的 $\frac{1}{3}$
$\text{C.}$ 输入端电压调为 $u=12 \sqrt{2} \sin (50 \pi t) V$
$\text{D.}$ 输入端电压调为 $u=6 \sqrt{2} \sin (100 \pi t) V$
多选题 (共 2 题 ),每题有多个选项正确
2025 年 4 月,我国已成功构建国际首个基于 DRO(远距离逆行轨道)的地月空间三星星座,DRO 具有"低能进入、稳定停泊、机动转移"的特点。若卫星甲从 DRO 变轨进入环月椭圆轨道,该轨道的近月点和远月点距月球表面的高度分别为 $a$ 和 $b$ ,卫星的运行周期为 $T$ ;卫星乙从 DRO 变轨进入半径为 $r$ 的环月圆形轨道,周期也为 $T$ 。月球的质量为 $M$ ,半径为 $R$ ,引力常量为 $G$ 。假设只考虑月球对甲、乙的引力,则( )
$\text{A.}$ $r=\frac{a+b+R}{2}$
$\text{B.}$ $r=\frac{a+b}{2}+R$
$\text{C.}$ $M=\frac{4 \pi^2 r^3}{G T^2}$
$\text{D.}$ $M=\frac{4 \pi^2 R^3}{G T^2}$
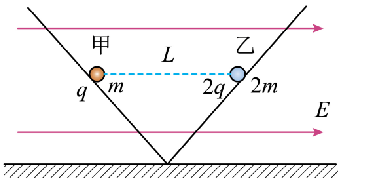
如图,两个倾角相等、底端相连的光滑绝缘轨道被固定在坚直平面内,空间存在平行于该坚直平面水平向右的匀强电场。带正电的甲、乙小球(均可视为质点)在轨道上同一高度保持静止,间距为 $L$ ,甲、乙所带电荷量分别为 $q 、 2 q$ ,质量分别为 $m 、 2 m$ ,静电力常量为 $k$ ,重力加速度大小为 g 。甲、乙所受静电力的合力大小分别为 $F_1 、 F_2$ ,匀强电场的电场强度大小为 $E$ ,不计空气阻力,则( )
$\text{A.}$ $F_1=\frac{1}{2} F_2$
$\text{B.}$ $E=\frac{k q}{2 L^2}$
$\text{C.}$ 若将甲、乙互换位置,二者仍能保持静止
$\text{D.}$ 若撤去甲,乙下滑至底端时的速度大小 $v=\sqrt{\frac{k q^2}{m L}}$
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
某实验小组通过实验探究加速度与力、质量的关系。
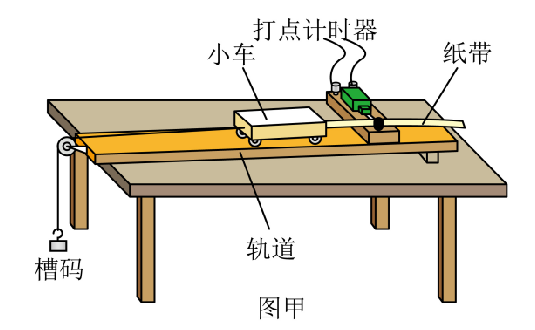
(1)利用图甲装置进行实验,要平衡小车受到的阻力。平衡阻力的方法是:调整轨道的倾斜度,使小车 $\qquad$。(选填正确答案标号)
a.能在轨道上保持静止
b.受牵引时,能拖动纸带沿轨道做匀速运动
c.不受牵引时,能拖动纸带沿轨道做匀速运动
(2)利用图乙装置进行实验,箱体的水平底板上安装有力传感器和加速度传感器,将物体置于力传感器上,箱体沿坚直方向运动。利用传感器测得物体受到的支持力 $F_{ N }$ 和物体的加速度 $a$ ,并将数据实时传送到计算机。
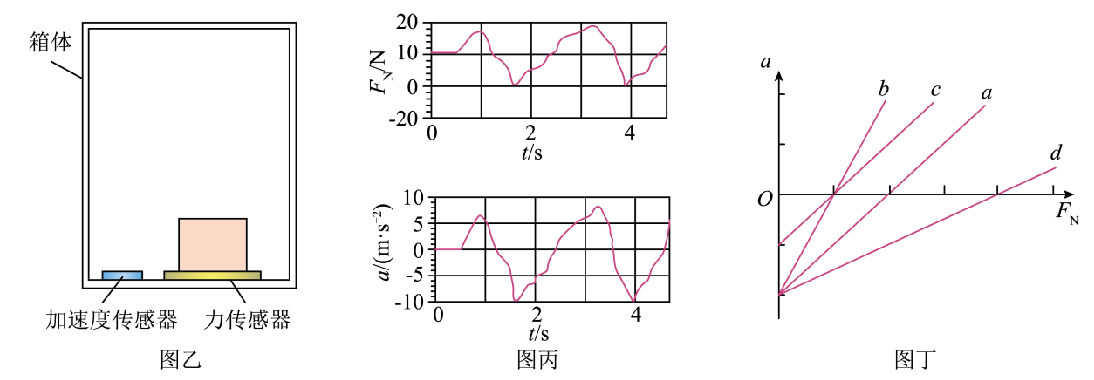
(1)图丙是根据某次实验采集的数据生成的 $F_{ N }$ 和 $a$ 随时间 $t$ 变化的散点图,以坚直向上为正方向。 $t=4 s$ 时,物体处于 $\qquad$ (选填"超重"或"失重")状态;以 $F_{ N }$ 为横轴、 $a$ 为纵轴,根据实验数据拟合得到的 $a-F_{ N }$ 图像为图丁中的图线 $a$ 、
(2)若将物体质量增大一倍,重新进行实验,其 $a-F_{ N }$ 图像为图丁中的图线 $\qquad$。(选填"$b$""$c$"或"$d$")
某同学设计了一个具有两种挡位("$\times 1$"挡和"$\times 10$"挡)的欧姆表,其内部电路如图甲所示。电源为电池组(电动势 $E$ 的标称值为 3.0 V ,内阻 $r$ 未知),电流表 G (表头)的满偏电流 $I_{ g }=20 mA$ ,内阻 $R_{ g }=45 \Omega$ ,定值电阻 $R_0=5 \Omega$ ,滑动变阻器 $R$ 的最大阻值为 $200 \Omega$ 。设计后表盘如图乙所示,中间刻度值为" 15 "。
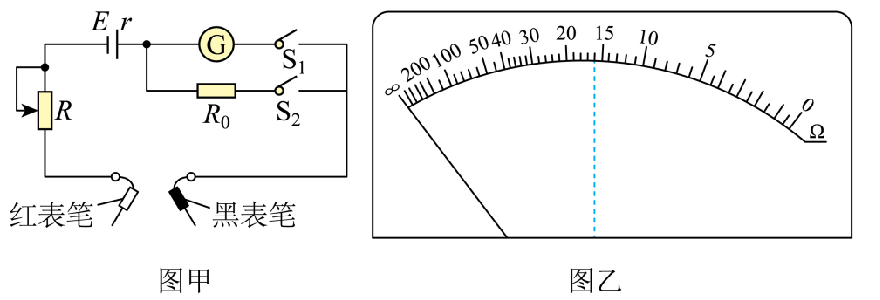
(1)测量前,要进行欧姆调零:将滑动变阻器的阻值调至最大,闭合开关 $S_1 、 S_2$ ,此时欧姆表处于"$\times 1$"挡,将红表笔与黑表笔 $\qquad$ ,调节滑动变阻器的阻值,使指针指向 $\qquad$ (选填" 0 "或"$\infty$")刻度位置。
(2)用该欧姆表对阻值为 $150 \Omega$ 的标准电阻进行试测,为减小测量误差,应选用欧姆表的 $\qquad$ (选填"$\times 1$"或"$\times 10$")挡。进行欧姆调零后,将电阻接在两表笔间,指针指向图乙中的虚线位置,则该电阻的测量值为 $\qquad$ $\Omega$ 。
(3)该同学猜想造成上述误差的原因是电源电动势的实际值与标称值不一致。为了测出电源电动势,该同学先将电阻箱以最大阻值(9999Л)接在两表笔间,接着闭合 $S_1$ 、断开 $S_2$ ,将滑动变阻器的阻值调到零,再调节电阻箱的阻值。当电阻箱的阻值调为 $228 \Omega$ 时,指针指向" 15 "刻度位置(即电路中的电流为 10 mA );当电阻箱的阻值调为 $88 \Omega$ 时,指针指向" 0 "刻度位置(即电路中的电流为 20 mA )。由测量数据计算出电源电动势为 $\qquad$ V 。(结果保留 2 位有效数字)
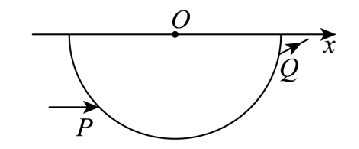
如图,玻璃砖的横截面是半径为 $R$ 的半圆,圆心为 $O$ 点,直径与 $x$ 轴重合。一束平行于 $x$ 轴的激光,从横截面上的 $P$ 点由空气射入玻璃砖,从 $Q$ 点射出。已知 $P$ 点到 $x$ 轴的距离为 $\frac{\sqrt{2}}{2} R, P 、 Q$ 间的距离为 $\sqrt{3} R$ 。
(1)求玻璃砖的折射率;
(2)在该横截面沿圆弧任意改变入射点的位置和入射方向,使激光能在圆心 $O$ 点发生全反射,求入射光线与 $x$ 轴之间夹角的范围。
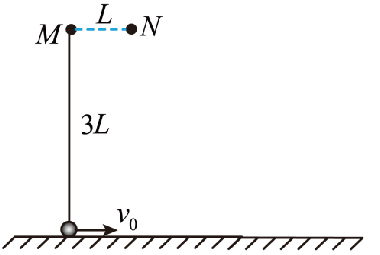
如图,$M 、 N$ 为固定在坚直平面内同一高度的两根细钉,间距 $L=0.5 m$ 。一根长为 $3 L$ 的轻绳一端系在 $M$ 上,另一端坚直悬挂质量 $m=0.1 kg$ 的小球,小球与水平地面接触但无压力。 $t=0$ 时,小球以水平向右的初速度 $v_0=10 m / s$开始在坚直平面内做圆周运动。小球牵引着绳子绕过 $N 、 M$ ,运动到 $M$ 正下方与 $M$ 相距 $L$ 的位置时,绳子刚好被拉断,小球开始做平抛运动。小球可视为质点,绳子不可伸长,不计空气阻力,重力加速度 g 取 $10 m / s ^2$ 。
(1)求绳子被拉断时小球的速度大小,及绳子所受的最大拉力大小;
(2)求小球做平抛运动时抛出点到落地点的水平距离;
(3)若在 $t=0$ 时,只改变小球的初速度大小,使小球能通过 $N$ 的正上方且绳子不松弛,求初速度的最小值。
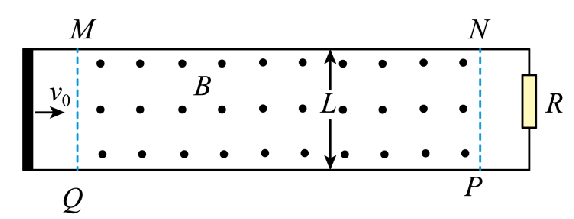
如图,平行光滑金属导轨被固定在水平绝缘桌面上,导轨间距为 $L$ ,右端连接阻值为 $R$ 的定值电阻。水平导轨上足够长的矩形区域 $M N P Q$ 存在坚直向上的匀强磁场,磁感应强度大小为 $B$ 。某装置从 $M Q$ 左侧沿导轨水平向右发射第 1 根导体棒,导体棒以初速度 $v_0$ 进入磁场,速度减为 0 时被锁定;从原位置再发射第 2 根相同的导体棒,导体棒仍以初速度 $v_0$ 进入磁场,速度减为 0 时被锁定,以此类推,直到发射第 $n$ 根相同的导体棒进入磁场。已知导体棒的质量为 $m$ ,电阻为 $R$ ,长度恰好等于导轨间距,与导轨接触良好(发射前导体棒与导轨不接触),不计空气阻力、导轨的电阻,忽略回路中的电流对原磁场的影响。
求:
(1)第1根导体棒刚进入磁场时,所受安培力的功率;
(2)第 2 根导体棒从进入磁场到速度减为 0 的过程中,其横截面上通过的电荷量;
(3)从第 1 根导体棒进入磁场到第 $n$ 根导体棒速度减为 0 的过程中,导轨右端定值电阻 $R$ 上产生的总热量。