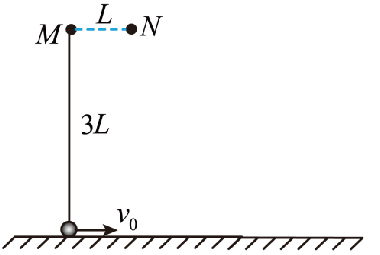
如图，$M 、 N$ 为固定在坚直平面内同一高度的两根细钉，间距 $L=0.5 m$ 。一根长为 $3 L$ 的轻绳一端系在 $M$ 上，另一端坚直悬挂质量 $m=0.1 kg$ 的小球，小球与水平地面接触但无压力。 $t=0$ 时，小球以水平向右的初速度 $v_0=10 m / s$开始在坚直平面内做圆周运动。小球牵引着绳子绕过 $N 、 M$ ，运动到 $M$ 正下方与 $M$ 相距 $L$ 的位置时，绳子刚好被拉断，小球开始做平抛运动。小球可视为质点，绳子不可伸长，不计空气阻力，重力加速度 g 取 $10 m / s ^2$ 。

（1）求绳子被拉断时小球的速度大小，及绳子所受的最大拉力大小；
（2）求小球做平抛运动时抛出点到落地点的水平距离；
（3）若在 $t=0$ 时，只改变小球的初速度大小，使小球能通过 $N$ 的正上方且绳子不松弛，求初速度的最小值。