单选题 (共 8 题 ),每题只有一个选项正确
样本数据 $2,8,14,16,20$ 平均数为()
$\text{A.}$ 8
$\text{B.}$ 9
$\text{C.}$ 12
$\text{D.}$ 18
已知 $z=1+ i$ ,则 $\frac{1}{z-1}=()$
$\text{A.}$ - i
$\text{B.}$ i
$\text{C.}$ -1
$\text{D.}$ 1
$A=\{-4,0,1,2,8\}, B=\left\{x \mid x^3=x\right\}, A \cap B=(\quad)$
$\text{A.}$ $\{0,1,2\}$
$\text{B.}$ $\{1,2,8\}$
$\text{C.}$ $\{2,8\}$
$\text{D.}$ $\{0,1\}$
不等式 $\frac{x-4}{x-1} \geqslant 2$ 解集是( )
$\text{A.}$ $\{x \mid-2 \leqslant x \leqslant 1\}$
$\text{B.}$ $\{x \mid x \leqslant-2\}$
$\text{C.}$ $\{x \mid-2 \leqslant x \lt1\}$
$\text{D.}$ $\{x \mid x>1\}$
在 $\triangle A B C$ 中,$B C=2, A C=1+\sqrt{3}, A B=\sqrt{6}, A=$( )
$\text{A.}$ $45^{\circ}$
$\text{B.}$ $60^{\circ}$
$\text{C.}$ $120^{\circ}$
$\text{D.}$ $135^{\circ}$
设抛物线 $C: y^2=2 p x(p>0)$ 的焦点 $F$ ,点 $A$ 在 $C$ 上,过 $A$ 作 $C$ 准线的垂线,垂足为 $B$ .若 $l_{B F}: y=-2 x+2$ ,则 $|A F|=()$
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 6
记 $S_n$ 为等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和,若 $S_3=6, S_5=-5, S_6=()$
$\text{A.}$ -20
$\text{B.}$ -15
$\text{C.}$ -10
$\text{D.}$ -5
已知 $0 < \alpha < \pi, \cos \frac{\alpha}{2}=\frac{\sqrt{5}}{5}$ ,则 $\sin \left(\alpha-\frac{\pi}{4}\right)=$( )
$\text{A.}$ $\frac{\sqrt{2}}{10}$
$\text{B.}$ $\frac{\sqrt{2}}{5}$
$\text{C.}$ $\frac{3 \sqrt{2}}{10}$
$\text{D.}$ $\frac{7 \sqrt{2}}{10}$
多选题 (共 3 题 ),每题有多个选项正确
记 $S_n$ 为等比 $\left\{a_n\right\}$ 的前 $n$ 项和,$q$ 为 $\left\{a_n\right\}$ 公比,$q>0$ ,若 $S_3=7, a_3=1$ ,则()
$\text{A.}$ $q=\frac{1}{2}$
$\text{B.}$ $a_5=\frac{1}{9}$
$\text{C.}$ $S_5=8$
$\text{D.}$ $a_n+S_n=8$
已知 $f(x)$ 定义在 R 上奇函数,且当 $x>0$ 时,$f(x)=\left(x^2-3\right) e^x+2$ ,则( )
$\text{A.}$ $f(0)=0$
$\text{B.}$ 当 $x < 0$ 时,$f(x)=-\left(x^2-3\right) e^{-x}-2$
$\text{C.}$ $f(x) \geqslant 2$ 当且仅当 $x \geqslant \sqrt{3}$
$\text{D.}$ $x=-1$ 是 $f(x)$ 极大值点
双曲线 $C: \frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0, b>0)$ 左、右焦点为 $F_1, F_2$ .左右顶点为 $A_1, A_2$ .以 $F_1 F_2$ 为直径的圆与 $C$ 的一条渐近线交于 $M 、 N$ ,且 $\angle N A_1 M=\frac{5 \pi}{6}$ ,则()
$\text{A.}$ $\angle A_1 M A_2=\frac{\pi}{6}$
$\text{B.}$ $\left|M A_1\right|=2\left|M A_2\right|$
$\text{C.}$ $C$ 离心率为 $\sqrt{13}$
$\text{D.}$ 当 $a=\sqrt{2}$ 时,四边形 $N A_1 M A_2$ 面积为 $8 \sqrt{3}$
填空题 (共 3 题 ),请把答案直接填写在答题纸上
已知平面向量 $\vec{a}=(x, 1), \vec{b}=(x-1,2 x), \vec{a} \perp(\vec{a}-\vec{b})$ ,则 $|\vec{a}|=$ $\qquad$ .
若 $x=2$ 是函数 $f(x)=(x-1)(x-2)(x-a)$ 极值点,则 $f(0)=$
一个底面半径为 4 cm ,高为 9 cm 的封闭圆柱形容器(容器壁厚度忽略不计)内有两个半径相等的铁球,则铁球半径的最大值为 $\qquad$ cm.
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $f(x)=\cos (2 x+\varphi)(0 \leq \varphi < \pi), f(0)=\frac{1}{2}$
(1)求 $\varphi$ ;
(2)设函数 $g(x)=f(x)+f\left(x-\frac{\pi}{6}\right)$ ,求 $g(x)$ 值域和单调区间.
已知椭圆 $C: \frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$ 的离心率为 $\frac{\sqrt{2}}{2}$ ,长轴长为 4 .
(1)求 $C$ 的方程.
(2)过点 $(0,-2)$ 的直线 $l$ 与 $C$ 交于 $A, B$ 两点,$O$ 为坐标原点.若 $S_{\triangle O A B}=\sqrt{2}$ ,求 $|A B|$【
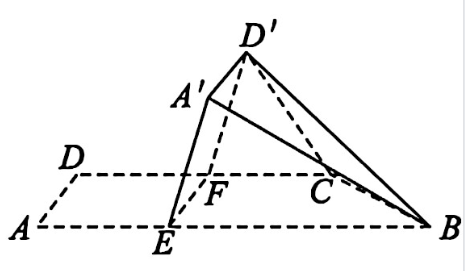
如图,四边形 $A B C D$ 中,$A B / / C D, \angle D A B=90^{\circ}, F$ 为 $C D$ 中点,点 $E$ 在 $A B$ 上, $E F / / A D, A B=3 A D, C D=2 A D$ .将四边形 $E F D A$ 沿 $E F$ 翻折至四边形 $E F D^{\prime} A^{\prime}$ ,使得面 $E F D^{\prime} A^{\prime}$ 与面 $E F C B$ 所成的二面角为 $60^{\circ}$ .
(1)证明:$A^{\prime} B / /$ 平面 $C D^{\prime} F$ .
(2)求面 $B C D^{\prime}$ 与面 $E F D^{\prime} A^{\prime}$ 所成二面角的正弦值.
已知函数 $f(x)=\ln (1+x)-x+\frac{1}{2} x^2-k x^3$ ,其中 $0 < k < \frac{1}{3}$ .
(1)证明:$f(x)$ 在 $(0,+\infty)$ 存在唯一的极值点和唯一零点
(2)设 $x_1, x_2$ 分别为 $f(x)$ 在 $(0,+\infty)$ 的极值点和零点
(i)设函数 $g(t)=f\left(x_1+t\right)-f\left(x_1-t\right)$ .证明:$g(t)$ 在 $\left(0, x_1\right)$ 单调递减;
(ii)比较 $2 x_1$ 与 $x_2$ 的大小,并证明.
甲、乙乒乓球练习,每个球胜者得 1 分,负者得 0 分.设每个球甲胜概率为 $p\left(\frac{1}{2} < p < 1\right)$ .乙胜概率为 $q, ~ p+q=1$ ,且各球胜负独立.对正整数 $k \geqslant 2$ ,记 $p_k$ 为打完 $k$ 个球后甲比乙至少多得 2 分的概率,$q_k$ 为打完 $k$ 个球后乙比甲至少多得 2 分的概率.
(1)求 $p_3, p_4$(用 $p$ 表示).
(2)若 $\frac{p_4-p_3}{q_4-q_3}=4$ ,求 $p$ .
(3)证明:对任意正整数 $m, ~ p_{2 m+1}-q_{2 m+1} < p_{2 m}-q_{2 m} < p_{2 m+2}-q_{2 m+2}$