单选题 (共 5 题 ),每题只有一个选项正确
设 $A$ 表示事件"物理及格,化学不及格",则其对立事件 $\bar{A}$ 表示
$\text{A.}$ "物理不及格或化学及格"
$\text{B.}$ "物理不及格,化学及格"
$\text{C.}$ "物理化学都及格或都不及格"
$\text{D.}$ "物理及格或化学不及格"
已知有 $P(B \mid A)=1$ ,则正确的是
$\text{A.}$ $B=\Omega$
$\text{B.}$ $P(B \mid \bar{A})=0$
$\text{C.}$ $A \supset B$
$\text{D.}$ $P(A \bigcup B)=P(B)$
设连续随机变量 X 的分布函数为 $\mathrm{F}(\mathrm{x})$ , a 为正数,则 $\mathrm{P}(|\mathrm{X}| \leqslant \mathrm{a})$ 等于
$\text{A.}$ $\mathrm{F}(\mathrm{a})+\mathrm{F}(-\mathrm{a})$
$\text{B.}$ $\mathrm{F}(\mathrm{a})+\mathrm{F}(-\mathrm{a})-1$
$\text{C.}$ $\mathrm{F}(\mathrm{a})-\mathrm{F}(-\mathrm{a})$
$\text{D.}$ $1-\mathrm{F}(\mathrm{a})+\mathrm{F}(-\mathrm{a})$
设 X 与 Y 为两个随机变量,则下列选项中能说明 X 与 Y 独立的是
$\text{A.}$ $E(X+Y)=E(X)+E(Y)$
$\text{B.}$ 对 $\forall a, b$ 有 $P(X \leqslant a, Y \leqslant b)=P(X \leqslant a) P(Y \leqslant b)$
$\text{C.}$ $\operatorname{Var}(\mathrm{X}+\mathrm{Y})=\operatorname{Var}(\mathrm{X})+\operatorname{Var}(\mathrm{Y})$
$\text{D.}$ $E(X Y)=E(X) E(Y)$
设总体 $X \sim N\left(\mu, \sigma^2\right)$ ,其中 $\mu$ 已知,$\sigma^2$ 未知,$\left(X_1, X_2, X_3\right)$ 为样本,则下列表达式中不是统计量的为
$\text{A.}$ $X_1+X_2+X_3$
$\text{B.}$ $\min \left(X_1, X_2, X_3\right)$
$\text{C.}$ $X_1+2 \mu$
$\text{D.}$ $\sum_{i=1}^3 \frac{X_i^2}{\sigma^2}$
填空题 (共 8 题 ),请把答案直接填写在答题纸上
袋中有 9 个黑球, 3 个白球,现每次取一个,无放回的取两次,则第二次取到的球是白球的概率为
已知 $P(A)=\frac{1}{3}, P(B \mid A)=\frac{1}{4}, P(A \mid B)=\frac{1}{6}$ ,则 $P(A \bar{B})=$ ,$P(A \bigcup B)=$
设 $X$ 的分布列为
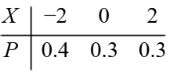
$E(X)=$ , $\operatorname{Var}(X)=$
设 $\boldsymbol{X}_1, \boldsymbol{X}_2, \cdots, \boldsymbol{X}_n$ 是取自总体 $N\left(\mu, \sigma^2\right)$ 的样本,则统计量 $\frac{\mathbf{1}}{\sigma^2} \sum_{i=1}^n\left(\boldsymbol{X}_i-\boldsymbol{\mu}\right)^2$ 服从 分布.
设 $x_1, \cdots, x_{10}$ 为来自 $X \sim \operatorname{Exp}(1 / 8)$ 的样本,则 $\operatorname{Var}(X)=$
设 X 服从正态分布, $\mathrm{E}(\mathrm{X})=0, \mathrm{P}(|\mathrm{X}| \leqslant 1)=0.5$ ,则 $\mathrm{P}(\mathrm{X} \leqslant 1)=$
设 $X_1, X_2, \cdots, X_n$ 为总体 $X$ 的样本,则总体方差 $\sigma^2$ 的一个无偏估计量为
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
一个袋子里面有 10 个白球和 90 个黑球,每次从袋子中不放回随机取一个球。(1)求在第一次和第二次都取得黑球的条件下,第三次也取得黑球的概率。(2)求在第一次和第三次都取得黑球的条件下,第二次取得黑球的概率。
某种产品由 20 个相同部件连接而成,每个部件的长度是均值为 2 mm 、标准差为 0.02 mm 的随机变量.假如这 20 个部件长度相互独立同分布,且规定产品总长为 40 $\pm 0.2 \mathrm{~mm}$ 为合格品,求该产品不合格品率.
设连续型随机变量 $X$ 的概率密度为
$$
f(x)=\left\{\begin{array}{cc}
A x+\frac{1}{2}, & 0 < x < 1 \\
0, & \text { 其它 }
\end{array}\right.
$$
(1)求常数 $A$ ;
(2)求数学期望 $E(X)$ ;
(3)求方差 $D(X)$ .
设随机变量 $(X, Y)$ 的概率密度为
$$
f(x, y)= \begin{cases}e^{-y}, & 0 < x < y ; \\ 0, & \text { 其它. }\end{cases}
$$
(1)求在 $Y=y$ 的条件下,$X$ 的条件概率密度;
(2)求概率 $P\{X+2 Y \leq 1\}, P\{0 \leq X \leq 1 / 2 \mid Y \leq 1\}, P\{X \geq 2 \mid Y=4\}$ .
设总体 $X$ 的概率密度为
$$
f(x ; \theta)=\left\{\begin{array}{cc}
(\theta+1) x^\theta, & 0 < x < 1, \\
0, & \text { 其它, }
\end{array}\right.
$$
其中 $\theta>1$ 为末知参数,又设 $\mathrm{x}_1, \mathrm{x}_2, \cdots, \mathrm{x}_{\mathrm{n}}$ 是 X 的一组样本观测值,求参数 $\theta$ 的极大似然估计值。