单选题 （共 8 题 ），每题只有一个选项正确
抛物线 $y=(x-2)^2+3$ 的对称轴是
$\text{A.}$ 直线 $x=-3$
$\text{B.}$ 直线 $x=3$
$\text{C.}$ 直线 $x=-2$
$\text{D.}$ 直线 $x=2$
二次函数 $y=a x^2+b x+c$ 的图象如右图，则点 $M\left(b, \frac{c}{a}\right)$ 在
$\text{A.}$ 第一象限
$\text{B.}$ 第二象限
$\text{C.}$ 第三象限
$\text{D.}$ 第四象限
已知二次函数 $y=a x^2+b x+c$, 且 $a < 0, a-b+c>0$, 则一定有
$\text{A.}$ $b^2-4 a c>0$
$\text{B.}$ $b^2-4 a c=0$
$\text{C.}$ $b^2-4 a c < 0$
$\text{D.}$ $b^2-4 a c \leqslant 0$
把抛物线 $y=x^2+b x+c$ 向右平移 3 个单位, 再向下平移 2 个单位, 所得图象的解析式是 $y=x^2-3 x+5$, 则有
$\text{A.}$ $b=3, c=7$
$\text{B.}$ $b=-9, c=-15$
$\text{C.}$ $b=3, c=3$
$\text{D.}$ $b=-9, c=21$
下面所示各图是在同一直角坐标系内, 二次函数 $y=a x^2+(a+c) x+c$ 与一次函数 $y=a x+c$ 的大致图象, 有且只有一个是正确的, 正确的是
$\text{A.}$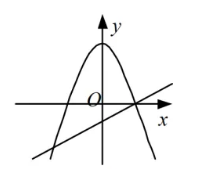 
$\text{B.}$ 
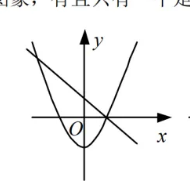$\text{C.}$ 
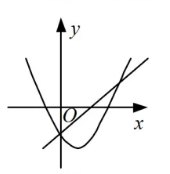$\text{D.}$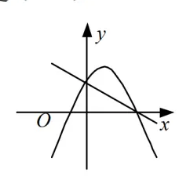 
抛物线 $y=x^2-2 x+3$ 的对称轴是直线
$\text{A.}$ $x=-2$
$\text{B.}$ $x=2$
$\text{C.}$ $x=-1$
$\text{D.}$ $x=1$
二次函数 $y=(x-1)^2+2$ 的最小值是
$\text{A.}$ -2
$\text{B.}$ 2
$\text{C.}$ -1
$\text{D.}$ 1
二次函数 $y=a x^2+b x+c$ 的图象如图所示, 若 $M=4 a+2 b+c N=a-b+c, P=4 a-b$, 则
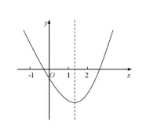
$\text{A.}$ $M>0, N>0, \quad P>0$
$\text{B.}$ $M < 0, N>0, \quad P>0$
$\text{C.}$ $M>0, \quad N < 0, \quad P>0$
$\text{D.}$ $M < 0, \quad N>0, \quad P < 0$
填空题 （共 4 题 ），请把答案直接填写在答题纸上
将 二次函数 $y=x^2-2 x+3$ 配方成 $y=(x-h)^2+k$ 的形式，则 $y=$
已知抛物线 $y=a x^2+b x+c$ 与 $x$ 轴有两个交点, 那么一元二次方程 $a x^2+b x+c=0$ 的根的情况是
已知抛物线 $y=a x^2+x+c$ 与 $x$ 轴交点的横坐标为 -1 , 则 $a+c=$
请你写出函数 $y=(x+1)^2$ 与 $y=x^2+1$ 具有的一个共同性质:
解答题 （共 7 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
已知函数 $y=x^2+b x-1$ 的图象经过点 $(3,2)$.
(1) 求这个函数的解析式;
(2) 当 $x>0$ 时, 求使 $y \geqslant 2$ 的 $x$ 的取值范围.
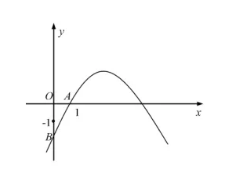
如右图, 抛物线 $y=-x^2+5 x+n$ 经过点 $A(1,0)$, 与 $y$ 轴交于点 $B$.
(1) 求抛物线的解析式;
(2) $P$ 是 $y$ 轴正半轴上一点, 且 $\triangle P A B$ 是以 $A B$ 为腰的等腰三角形, 试求点 $P$ 的坐标.
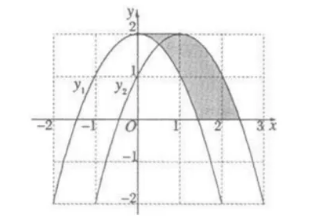
如图, 抛物线 $\mathrm{y}_1=-\mathrm{x}^2+2$ 向右平移 1 个单位得到抛物线 $\mathrm{y}_2$, 回答下列问题:
(1) 抛物线 $\mathrm{y}_2$ 的顶点坐标
（2）阴影部分的面积 $S=$
(3) 若再将抛物线 $\mathrm{y}_2$ 绕原点 $\mathrm{O}$ 旋转 $180^{\circ}$ 得到抛物线 $\mathrm{y}_3$, 求抛物线 $\mathrm{y}_3$ 的解析式.
如图, 已知抛物线 $y=a x^2+b x+\sqrt{3}$ 交 $x$ 轴正半轴于 $A, B$ 两点, 交 $y$ 轴于点 $\mathrm{C}$,且 $\angle \mathrm{CBO}=60^{\circ}, \angle \mathrm{CAO}=45^{\circ}$, 求抛物线的解析式和直线 $\mathrm{BC}$ 的解析式.
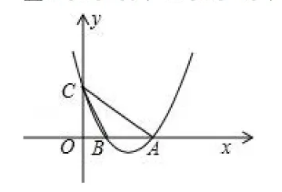
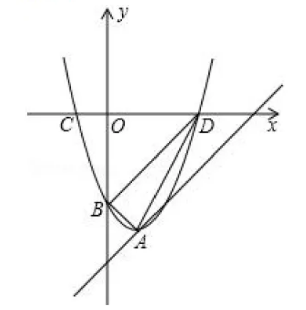
如图, 抛物线 $y=x^2+b x-c$ 经过直线 $y=x-3$ 与坐标轴的两个交点 $A, B$, 此抛物线与 $x$ 轴的另一个交点为 $\mathrm{C}$, 抛物线的顶点为 $\mathrm{D}$.
(1) 求此抛物线的解析式;
(2) 点 $P$ 为抛物线上的一个动点, 求使 $S_{\triangle A P C}: S_{\triangle A C D}=5: 4$ 的点 $P$ 的坐标.
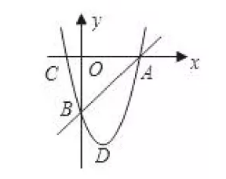
如图, 抛物线 $y=a(x+1)^2$ 的顶点为 $\mathrm{A}$, 与 $\mathrm{y}$ 轴的负半轴交于点 $\mathrm{B}$, 且 $\mathrm{OB}=\mathrm{OA}$.
(1) 求抛物线的解析式;
(2) 若点 $\mathrm{C}(-3, \mathrm{~b})$ 在该抛物线上, 求 $\mathrm{S}_{\triangle \mathrm{ABC}}$ 的值.
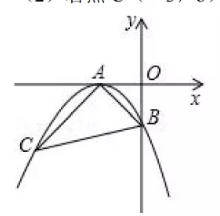
如图, 抛物线 $y=x^2-2 x+c$ 的顶点 $\mathrm{A}$ 在直线 $1: \mathrm{y}=\mathrm{x}-5$ 上.
(1) 求抛物线顶点 $\mathrm{A}$ 的坐标及 $\mathrm{c}$ 的值;
(2) 设抛物线与 $y$ 轴交于点 $B$, 与 $x$ 轴交于点 $C 、 D$ ( $C$ 点在 $D$ 点的左侧), 试判断 $\triangle A B D$的形状.
