已知集合 $A=\{0,1,2\}, B=\{x \mid x=3 k-1, k \in \mathbf{N}\}$, 则 $A \cap B=$

若复数 $z$ 满足: $z+2 \bar{z}=3-2 i$, 则 $|z|$ 为

已知等差数列 $\left\{a_n\right\}$ 的前 $n$ 项和为 $S_n$, 且 $2 S_n=2 a_n+n^2-1$.
(1) 求 $a_n$;
(2) 求数列 $\left\{\frac{1}{a_n a_{n+1}}\right\}$ 的前 $n$ 项和 $T_n$.

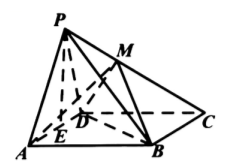
如图, 在四棱椎 $P-A B C D$ 中, 四边形 $A B C D$ 是边长为 2 的正方形, 平面 $P A D \perp$ 平面 $A B C D$, $P A=P D=\sqrt{5}$, 点 $E$ 是线段 $A D$ 的中点, $\overrightarrow{C M}=2 \overrightarrow{M P}$.
(1) 证明: $P E / /$ 平面 $B D M$;
(2) 求平面 $A M B$ 与平面 $B D M$ 的夹角.

某工厂生产某种元件, 其质量按测试指标划分为: 指标大于或等于 82 为合格品, 小于 82 为次品, 现抽取这种元件 100 件进行检测, 检测结果统计如下表:

(1) 现从这 100 件样品中随机抽取 2 件, 若其中一件为合格品, 求另一件也为合格品的概率;
(2) 关于随机变量, 俄国数学家切比雪夫提出切比雪夫不等式:
若随机变量 $X$ 具有数学期望 $E(X)=\mu$, 方差 $D(X)=\sigma^2$, 则对任意正数 $\varepsilon$, 均有 $P(|x-\mu| \geq \varepsilon) \leq \frac{\sigma^2}{\varepsilon^2}$ 成立.
(i) 若 $X \sim B\left(100, \frac{1}{2}\right)$, 证明: $P(0 \leq X \leq 25) \leq \frac{1}{50}$;
(ii) 利用该结论表示即使分布未知, 随机变量的取值范围落在期望左右的一定范围内的概率是有界的.若该工厂声称本厂元件合格率为 $90 \%$, 那么根据所给样本数据, 请结合“切比雪夫不等式”说明该工厂所提供的合格率是否可信? (注: 当随机事件 $A$ 发生的概率小于 0.05 时, 可称事件 $A$ 为小概率事件)

已知椭圆 $L: \left.\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0) \right\rvert\,$ 的左项点 $A(-3,0)$ 和下顶点 $B$, 焦距为 $4 \sqrt{2}$, 直线 $l$ 交椭圆 $L$ 于 $C, D$ (不同于椭圆的顶点）两点，直线 $A D$ 交 $y$ 轴于 $M$, 直线 $B C$ 交 $x$ 轴于 $N$, 且直线 $M N$ 交 $l$ 于 $P$.
(1) 求椭圆 $L$ 的标准方程;
(2) 若直线 $A D, B C$ 的斜率相等, 证明: 点 $P$ 在一条定直线上运动.

①在微积分中, 求极限有一种重要的数学工具一洛必达法则, 法则中有结论: 若函数 $f(x), g(x)$ 的导函数分别为 $f^{\prime}(x), g^{\prime}(x)$, 且 $\lim _{x \rightarrow a} f(x)=\lim _{x \rightarrow a} g(x)=0$, 则 $\lim _{x \rightarrow a} \frac{f(x)}{g(x)}=\lim _{x \rightarrow a} \frac{f^{\prime}(x)}{g^{\prime}(x)}$.
②设 $a>0, k$ 是大于 1 的正整数, 若函数 $f(x)$ 满足: 对任意 $x \in[0, a]$, 均有 $f(x) \geq f\left(\frac{x}{k}\right)$ 成立, 且 $\lim _{x \rightarrow 0} f(x)=0$, 则称函数 $f(x)$ 为区间 $[0, a]$ 上的 $k$ 阶无穷递降函数.
结合以上两个信息, 回答下列问题:
(1) 试判断 $f(x)=x^3-3 x$ 是否为区间 $[0,3]$ 上的 2 阶无穷递降函数;
(2) 计算: $\lim _{x \rightarrow 0}(1+x)^{\frac{1}{x}}$;
(3) 证明: $\left(\frac{\sin x}{x-\pi}\right)^3 < \cos x, x \in\left(\pi, \frac{3}{2} \pi\right)$.