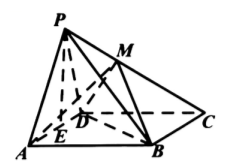
如图, 在四棱椎 $P-A B C D$ 中, 四边形 $A B C D$ 是边长为 2 的正方形, 平面 $P A D \perp$ 平面 $A B C D$, $P A=P D=\sqrt{5}$, 点 $E$ 是线段 $A D$ 的中点, $\overrightarrow{C M}=2 \overrightarrow{M P}$.
(1) 证明: $P E / /$ 平面 $B D M$;
(2) 求平面 $A M B$ 与平面 $B D M$ 的夹角.
(1) 证明: $P E / /$ 平面 $B D M$;
(2) 求平面 $A M B$ 与平面 $B D M$ 的夹角.
