定义在 $[0,1]$ 上的函数 $f(x)$ 满足: $\forall x \in[0,1], f(1-x)+f(x)=1$, 且 $f\left(\frac{x}{3}\right)=\frac{1}{2} f(x), f(0)=0$, 当 $0 \leq x_1 < x_2 \leq 1$ 时, $f\left(x_1\right) \leq f\left(x_2\right)$, 则

已知函数 $f(x)=a x^2-x-\ln x$, 其中 $a \in \mathrm{R}$.
(1) 若 $a=1$, 求 $f(x)$ 的极值
(2) 是否存在实数 $a$, 使 $f(x)$ 在 $(0,1)$ 内单调? 若存在, 求出 $a$ 的取值范围; 若不存在, 请说明理由:

如图, 圆柱上, 下底面圆的圆心分别为 $O, O_1$, 该圆柱的轴截面为正方形, 三棱柱 $A B C-A_1 B_1 C_1$ 的三条侧棱均为圆柱的母线, 且 $A B=A C=\frac{\sqrt{30}}{6} O O_1$, 点 $P$ 在轴 $O O_1$ 上运动.

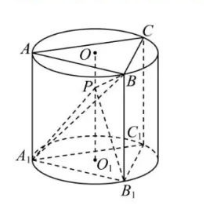
(1) 证明: 不论 $P$ 在何处, 总有 $B C \perp P A_1$;
(2) 当 $P$ 为 $O O_1$ 的中点时, 求平面 $A_1 P B$ 与平面 $B_1 P B$ 夹角的余弦值.

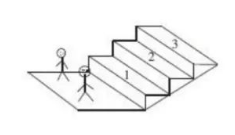
如图, 小华和小明两个小伙伴在一起做游戏, 他们通过划拳 (剪刀、石头、布) 比赛决胜谁首先登上第 3 个台阶, 他们规定从平地开始, 每次划拳赢的一方登上一级台阶, 输的一方原地不动, 平局时两个人都上一级台阶, 如果一方连续两次赢, 那么他将额外获得一次上一级台阶的奖励, 除非已经登上第 3 个台阶, 当有任何一方登上第 3 个台阶时, 游戏结束, 记此时两个小伙伴划拳的次数为 $X$.
(1) 求游戏结束时小华在第 2 个台阶的概率;
(2) 求 $X$ 的分布列和数学期望.

已知椭圆 $C_1: \frac{x^2}{8}+\frac{y^2}{4}=1$ 与椭圆 $C_2$ 有相同的离心率, 椭圆 $C_2$ 焦点在 $y$ 轴上且经过点 $(1, \sqrt{2})$.
(1) 求椭圆 $C_2$ 的标准方程;
(2) 设 $A$ 为椭圆 $C_1$ 的上顶点, 经过原点的直线 $l$ 交椭圆 $C_2$ 于 $P 、 Q$, 直线 $A P 、 A Q$ 与椭圆 $C_1$ 的另一

个交点分别为点 $M$ 和 $N$, 若 $\triangle A M N$ 与 $\triangle A P Q$ 的面积分别为 $S_1$ 和 $S_2$, 求 $\frac{S_1}{S_2}$ 的取值范围.

设正整数 $n \geq 3$, 有穷数列 $\left\{a_n\right\}$ 满足 $a_i>0(i=1,2, \cdots, n)$, 且 $a_1+a_2+\cdots+a_n=n$, 定义积值 $S=a_1 \cdot a_2 \cdots \cdots a_n$.
(1) 若 $n=3$ 时, 数列 $\left\{\frac{1}{2}, 1, \frac{3}{2}\right\}$ 与数列 $\left\{\frac{1}{6}, \frac{2}{3}, \frac{13}{6}\right\}$ 的 $S$ 的值分别为 $S_1, S_2$.
(1)试比较 $S_1$ 与 $S_2$ 的大小关系;
(2) 若数列 $\left\{a_n\right\}$ 的 $S$ 满足 $\min \left\{S_1, S_2\right\} < S < \max \left\{S_1, S_2\right\}$, 请写出一个满足条件的 $\left\{a_n\right\}$;
(2) 若 $n=4$ 时, 数列 $\left\{a_1, a_2, a_3, a_4\right\}$ 存在 $i, j \in\{1,2,3,4\}$, 使得 $a_i < 1 < a_j$, 将 $a_i, a_j$ 分别调整为 $a_i^{\prime}=a_i+a_j-1, a_j^{\prime}=1$, 其它 2 个 $a_k(k \neq i, j)$, 令 $a_k^{\prime}=a_k$. 数列 $\left\{a_1, a_2, a_3, a_4\right\}$ 调整前后的积值分别为 $S, S^{\prime}$,写出 $S, S^{\prime}$ 的大小关系并给出证明:
(3) 求 $S=a_1 \cdot a_2 \cdots \cdots a_n$ 的最大值, 并确定 $S$ 取最大值时 $a_1, a_2, \cdots, a_n$ 所满足的条件, 并进行证明.