单选题 (共 10 题 ),每题只有一个选项正确
式子 $\frac{\sqrt{2 x+1}}{x-1}$ 有意义的 $x$ 取值范围是
$\text{A.}$ $x \neq 1$
$\text{B.}$ $x \geq-\frac{1}{2}$
$\text{C.}$ $x \geq-\frac{1}{2}$ 且 $x \neq 1$
$\text{D.}$ $x>-\frac{1}{2}$ 且 $x \neq 1$
在二次根式 $2 \sqrt{x y}, \sqrt{8}, \sqrt{\frac{x}{2}}, \sqrt{2 x^2}$ 中, 最简二次根式的个数
$\text{A.}$ 4
$\text{B.}$ 3
$\text{C.}$ 2
$\text{D.}$ 1
如图, 已知正方形的边长为单位长度, 以表示数 1 的点为圆心, 正方形对角线长为半径画弧, 交数轴于点 $A$, 则点 $A$ 表示的数是
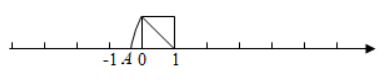
$\text{A.}$ $-\frac{1}{2}$
$\text{B.}$ $-\frac{1}{3}$
$\text{C.}$ $1-\sqrt{3}$
$\text{D.}$ $1-\sqrt{2}$
化简 $\sqrt{4 x^2-4 x+1}-(\sqrt{2 x-3})^2$ 得
$\text{A.}$ $2$
$\text{B.}$ $-4 x+4$
$\text{C.}$ $-2$
$\text{D.}$ $4 x-4$
如图所示, $\square A B C D$ 中, 对角线 $A C, B D$ 交于点 $O, E$ 是 $C D$ 中点, 连接 $O E$, 若 $O E=3 \mathrm{~cm}$, 则 $A D$ 的长为
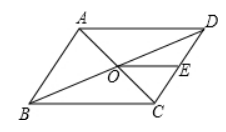
$\text{A.}$ $3 \mathrm{~cm}$
$\text{B.}$ $6 \mathrm{~cm}$
$\text{C.}$ $9 \mathrm{~cm}$
$\text{D.}$ $12 \mathrm{~cm}$
“赵爽弦图”巧妙地利用面积关系证明了勾股定理, 是我国古代数学的骄傲. 如图所示的“赵爽弦图” 是由四个全等的直角三角形和一个小正方形拼成的一个大正方形. 设直角三角形较长直角边长为 $a$, 较短直角边长为 $b$. 若 $a b=6$, 大正方形的面积为 16 , 则小正方形的面积为
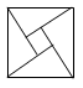
$\text{A.}$ 8
$\text{B.}$ 6
$\text{C.}$ 4
$\text{D.}$ 3
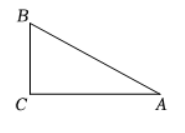
如图, 山坡 $A B$ 的高 $B C$ 为 $5 \mathrm{~cm}$, 水平距离 $A C$ 为 $12 \mathrm{~m}$, 若在山坡上每隔 $0.65 \mathrm{~m}$ 栽一棵树, 则从上到下共栽树 (山顶, 山脚均要栽)
$\text{A.}$ 19棵
$\text{B.}$ 20棵
$\text{C.}$ 21棵
$\text{D.}$ 22棵
已知 $a=\sqrt{3}-\sqrt{2}, b=\sqrt{3}+\sqrt{2}$, 那么 $a$ 与 $b$ 的关系为
$\text{A.}$ 互为相反数
$\text{B.}$ 互为倒数
$\text{C.}$ 相等
$\text{D.}$ $a$ 是 $b$ 的平方根
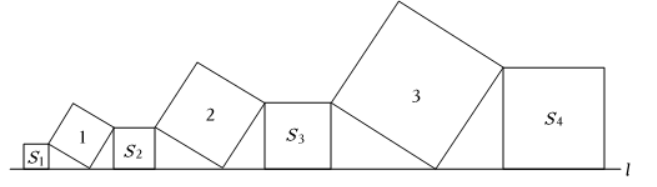
在直线 $l$ 上依次摆着几个正方形 (如图), 已知斜放的三个正方形的面积分别为 $1,2,3$, 正放的四个正方形的面积分别是 $S_1, S_2, S_3, S_4$, 则 $S_1+S_2+S_3+S_4$ 等于
$\text{A.}$ 3
$\text{B.}$ 4
$\text{C.}$ 5
$\text{D.}$ 6
$\triangle A B C$ 的三边分别为 $a, b, c$, 下列条件能推出 $\triangle A B C$ 是直角三角形的有
(1) $a^2-c^2=b^2$ ;
(2) $(a-b)(a+b)+c^2=0$;
(3) $\angle A=\angle B-\angle C$;
(4) $\angle A: \angle B: \angle C=1: 2: 3$;
(5) $a=\frac{1}{3}, b=\frac{1}{4}, c=\frac{1}{5}$;
(6) $a=1$ $0, b=24, c=26$.
$\text{A.}$ 2个
$\text{B.}$ 3个
$\text{C.}$ 4个
$\text{D.}$ 5个
填空题 (共 8 题 ),请把答案直接填写在答题纸上
已知 $\sqrt{-\frac{1}{m}}$ 有意义, 那么点 $(m, \sqrt{-m})$ 在平面直角坐标系中的第 ________ 象限.
如图, 在平行四边形 $A B C D$ 中, $A B=\sqrt{13}, A D=4$, 将其沿 $A E$ 翻折后, 点 $B$ 恰好与点 $C$ 重合, 则折痕 $A E$ 的长为

已知命题:“如果两个三角形全等, 那么这两个三角形的面积相等. ” 写出它的逆命题: ________ , 该逆命题是 ________ 命题
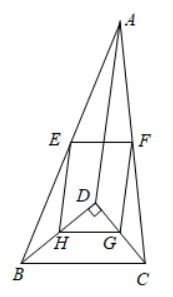
如图, $D$ 是 $\triangle A B C$ 内一点, $B D \perp C D, A D=7, B D=4, C D=3, E 、 F 、 G 、 H$ 分别是 $A B 、 A C 、 C$ $D 、 B D$ 的中点, 则四边形 $E F G H$ 的周长是
已知直线 $a / / b$, 若直线 $a$ 上的一点 $A$ 到直线 $b$ 的距离为 $2 \mathrm{~cm}$, 则直线 $b$ 上一点 $B$ 到直线 $a$ 的距离是
如果最简二次根式 $\sqrt{1+a}$ 与 $\sqrt{2 a-3}$ 可以合并, 那么 $a=$
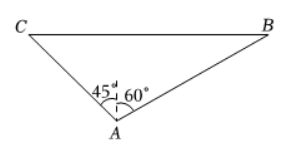
如图所示, 一艘轮船在小岛 $A$ 的北偏东 $60^{\circ}$ 方向距小岛 80 海里的 $B$ 处, 沿正西方向航行 3 小时后到达位于小岛北偏西 $45^{\circ}$ 方向的 $C$ 处, 则轮船行驶的速度为 ________ 海里/小时.
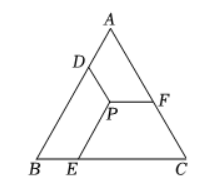
如图, 已知等边三角形 $A B C$ 的边长为 $8, P$ 是 $\triangle A B C$ 内一点, $P D / / A C, P E / / A B, P F / / B C$, 点 $D$, $E, F$ 分别在 $A B, B C, A C$ 上, 则 $P D+P E+P F=$
解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
计算:
( 1) $\left(\frac{1}{3} \sqrt{27}-\sqrt{24}-3 \sqrt{\frac{2}{3}}\right) \div \sqrt{12}$.
(2) $\sqrt{30} \times \frac{3}{2} \sqrt{2 \frac{2}{3}} \div 2 \sqrt{2 \frac{1}{2}}$.
已知 $a=3+\sqrt{2}, b=3-\sqrt{2}$, 分别求下列代数式的值:
(1) $a^2-b^2$;
(2) $a^2 b+a b^2$.
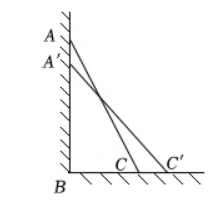
如图, 一架梯子长 $A C=2.5$ 米, 斜靠在一面墙上, 梯子底端与墙的距离 $B C=0.7$ 米.
(1) 这个梯子的顶端距地面有多高?
(2) 如果这个梯子的顶端下滑了 0.4 米至 $A^{\prime}$ 处, 那梯子的底部在水平方向也滑动了 0.4 米吗?
观察下列运算过程:
$$
\begin{aligned}
& \frac{1}{1+\sqrt{2}}=\frac{1}{\sqrt{2}+1}=\frac{\sqrt{2}-1}{(\sqrt{2}+1)(\sqrt{2}-1)}=\frac{\sqrt{2}-1}{(\sqrt{2})^2-1^2}=\sqrt{2}-1 \\
& \frac{1}{\sqrt{2}+\sqrt{3}}=\frac{1}{\sqrt{3}+\sqrt{2}}=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3}+\sqrt{2})(\sqrt{3}-\sqrt{2})}=\frac{\sqrt{3}-\sqrt{2}}{(\sqrt{3})^2-(\sqrt{2})^2}=\sqrt{3}-\sqrt{2}
\end{aligned}
$$
请运用上面的运算方法计算:
$$
\frac{1}{1+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{5}}+\frac{1}{\sqrt{5}+\sqrt{7}}+\ldots+\frac{1}{\sqrt{2015}+\sqrt{2017}}+\frac{1}{\sqrt{2017}+\sqrt{2019}}=
$$
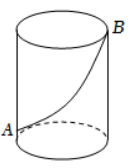
如图, 有一个圆柱形无盖油罐, 它的底面周长为 24 米, 高为 6 米, 一只老鼠从距底面 1 米的 $A$ 处沿油罐侧面爬行到对面 $B$ 处偷吃, 则它爬行的最短路程为多少?
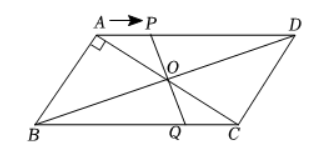
如图, 平行四边形 $A B C D$ 的对角线 $A C 、 B D$ 相交于点 $O, A B \perp A C, A B=3, B C=$ 5 , 点 $P$ 从点 $A$ 出发, 沿 $A D$ 以每秒 1 个单位的速度向终点 $D$ 运动. 连接 $P O$ 并延长交 $B C$ 于点 $Q$. 设点 $P$ 的运动时间为 $t$ 秒。
(1) 求 $B Q$ 的长; (用含 $t$ 的代数式表示)
(2) 当四边形 $A B Q P$ 是平行四边形时, 求 $t$ 的值;
(3) 当点 $O$ 在线段 $A P$ 的垂直平分线上时, 直接写出 $t$ 的值.