单选题 (共 6 题 ),每题只有一个选项正确
在物理学发展的历程中, 许多科学家的科学研究为物理学的建立做出了巨大贡献。下列叙述中正确的是
$\text{A.}$ 松香在熔化过程中温度保持不变, 松香分子的平均动能会变大
$\text{B.}$ 2023 年的诺贝尔物理学奖授予 “采用实验方法产生阿秒脉冲光的技术”, 阿秒脉冲光是一种非常短的光脉冲, 其持续时间在阿秒的量级, 即 $10^{-18} \mathrm{~s}$, 阿秒对应的物理量不是国际单位制的基本量
$\text{C.}$ 法拉第提出了电场的观点, 其实电场以及磁场是一种客观存在, 变化的电磁场和分子、原子组成的实物一样具有能量和动量
$\text{D.}$ 德国物理学家普朗克为解释物体热辐射规律, 提出了. 能量子的假说, 他同时最早发现了光电效应,爱因斯坦由于发现了光电效应的规律而获得诺贝尔物理学奖
高空中, 一架飞机沿水平方向做匀加速直线运动, 加速度大小为 $1 \mathrm{~m} / \mathrm{s}^2$, 每隔 $1 \mathrm{~s}$ 从飞机上落下一物体, 不计空气阻力, 重力加速度取 $10 \mathrm{~m} / \mathrm{s}^2$, 这些物体在空中排列的图线是一条
$\text{A.}$ 倾斜直线, 直线的斜率为 10
$\text{B.}$ 倾斜直线, 直线的斜率为 $\frac{1}{10}$
$\text{C.}$ 坚直直线
$\text{D.}$ 抛物线, 其竖直分运动是自由落体
如图所示, 坚直墙壁上固定一支架 $M O N$, 其中水平杆 $O M$ 表面粗䊁, 倾斜杆 $O N$ 表面光滑。杆 $O M 、$ 、杆 $O N$ 上分别套有小环 $P 、 Q$, 两环由不可伸长的轻质细绳相连,处于平衡状态, 现将 $P$ 环向右移动少许重新达到平衡。那么移动后的平衡状态和原来的平衡状态 (图示状态) 相比较, 下列说法正确的是
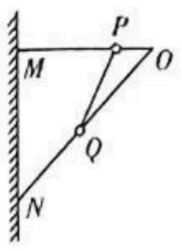
$\text{A.}$ 杆 $O N$ 对环 $Q$ 的弹力一定变大
$\text{B.}$ 细绳的拉力可能变大
$\text{C.}$ 环 $P$ 与杆 $O M$ 间的弹力一定变大
$\text{D.}$ 环 $P$ 的摩擦力可能不变
如图甲, “星下点” 是指卫星和地心莲线与地球表面的交点。图乙是航天控制中心大屏幕上显示卫星 FZO1 的“星下点”在一段时间内的轨迹,已知地球同步卫星的轨道半径为 $r=6.6 R(R$是地球的半径), FZO1 绕行方向与地球自转方向一致,则下列说法正确的是
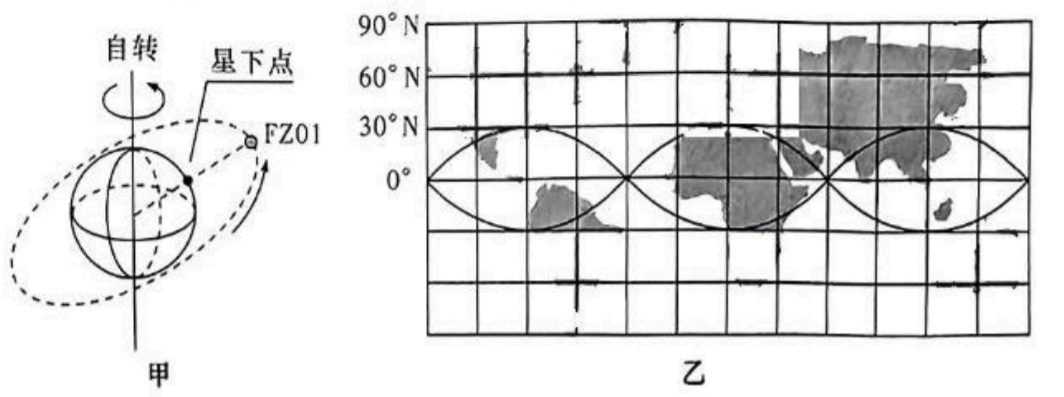
$\text{A.}$ 卫星 FZ01 的轨道半径约为 $\frac{r}{3}$
$\text{B.}$ 卫星 FZ01 的轨道半径约为 $\frac{r}{5}$
$\text{C.}$ 卫星 FZ01 可以记录到南极点的气候变化
$\text{D.}$ 卫星 FZ01 不可以记录到北极点的气候变化
无线充电宝可通过磁吸力吸附在手机背面, 如图甲所示为科创小组某同学手握手机 (手不接触充电宝), 利用手机软件记录坚直放置的手机及吸附的充电宝从静止开始在坚直方向上的一次变速运动过程 (手机与充电宝始终相对静止), 记录的加速度 $a$ 随时间 $t$ 变化的图像如图乙所示 (规定向上为正方向), $t_2$ 时刻充电宝速度为零, 且最终处于静止状态。已知手机的质量为 $0.3 \mathrm{~kg}$, 无线充电宝质量为 $0.2 \mathrm{~kg}$, 手机与充电宝之间的动摩擦因数 $\mu=0.5$, 最大静摩擦力等于滑动摩擦力, 重力加速度 $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$ 。在该过程中下列说法正确的是
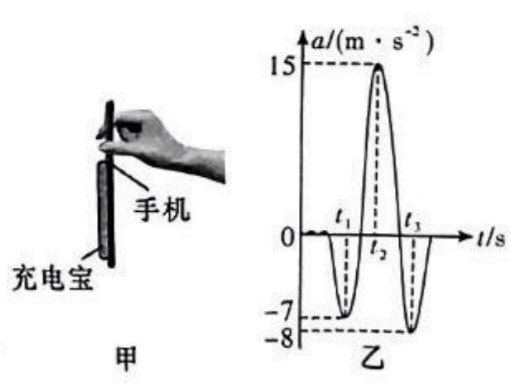
$\text{A.}$ 充电宝在 $t_1$ 与 $t_2$ 时刻所受的摩擦力方向相反
$\text{B.}$ $t_3$ 时刻充电宝受的摩擦力大小为 $3.6 \mathrm{~N}$
$\text{C.}$ 充电宝受到的静摩擦力的最大值为 $7.5 \mathrm{~N}$
$\text{D.}$ 充电宝与手机之间的吸引力大小至少为 $10 \mathrm{~N}$
如图所示, 固定光滑斜面倾角 $\theta=60^{\circ}$, 其底端与竖直面内半径为 $R$ 的固定光滑圆弧轨道相切, 位置 $D$ 为圆弧轨道的最低点。质量为 $2 m$ 的小球 $A$ 和质量为 $m$ 的小环 $B$ (均可视为质点) 用 $L=1.5 R$ 的轻杆通过轻质较链相连。 $B$ 套在光滑的固定竖直长杆上, 杆和圆轨道在同一坚直平面内, 杆过轨道圆心 $O$, 初始轻杆与斜面垂直。在斜面上由静止释放 $A$, 假设在运动过程中两杆不会碰撞, 小球能滑过 $D$ 点且通过轨道连接处时无能量损失 (速度大小不变), 重力加速度为 $g$, 从小球 $A$ 由静止释放到运动至最低点的过程中, 下列判断正确的是
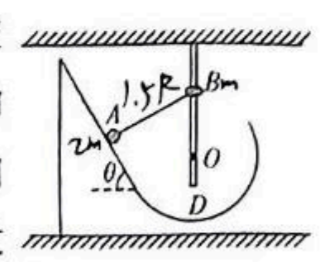
$\text{A.}$ $A$ 和 $B$ 组成的系统的机械能不守恒
$\text{B.}$ 刚释放时小球 $A$ 的加速度大小为 $\frac{\sqrt{3}}{2} g$
$\text{C.}$ 小环 $B$ 速度最大时轻杆弹力为 $m g$
$\text{D.}$ 小球 $A$ 运动到最低点时的速度大小为 $\frac{\sqrt{3 g R}}{3}$
多选题 (共 4 题 ),每题有多个选项正确
一列绳波在水平方向上传播, 现对其频闪照相, 拍摄频率为 $5 \mathrm{~Hz}$ 。在同一底片上多次曝光后形成照片如图所示, 照片与实物比例为 $1 1 00$ 。照片中 $A 、 B 、 C 、 D$ 四点为同一水平线上的四点, 且 $A B$ $=B C=C D=2 \mathrm{~cm}$ 。 以下说法正确的是
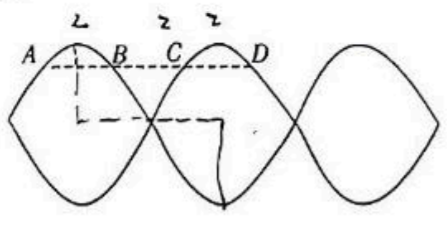
$\text{A.}$ 该绳波波长为 $4 \mathrm{~m}$
$\text{B.}$ 该绳波波速可能为 $60 \mathrm{~m} / \mathrm{s}$
$\text{C.}$ 该波可能与周期为 $0.1 \mathrm{~s}$ 的另一列绳波发生干涉
$\text{D.}$ 同一次曝光时 $A 、 C$ 两处质点振动方向相反
如图所示, 四边形 $a b c d$ 中, $a b=a d, c d=c b, a d$ 垂直 $d c 、 a b$ 垂直 $b c, \angle c=$ $120^{\circ}, O$ 点和 $c$ 点关于直线 $b d$ 对称, $O c$ 连线与 $d b$ 连线的交点为 $e$ (未标出)。在 $a, b$ 和 $d$ 点各固定一个带电荷量为 $q$ 的正电荷, $O$ 点和 $c$ 点的电势分别为 $\varphi_1$ 和 $\varphi_2$ 。下列说法正确的是
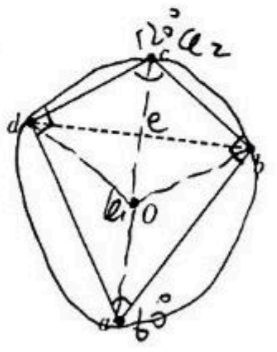
$\text{A.}$ $c$ 点的电场强度方向由 $O$ 指向 $c$, 且小于 $e$ 点的电场强度大小
$\text{B.}$ 若仅将 $a$ 点的正电荷换成带相同电荷量的负电荷, 则 $c$ 点电势等于 $\frac{4}{3} \varphi_1-\varphi_2$
$\text{C.}$ 若仅将 $b$ 点的正电荷换成带相同电荷量的负电荷, 则 $c$ 点电势等于 $\varphi_2-\frac{1}{2} \varphi_1$
$\text{D.}$ 电子在 $O$ 点的电势能小于在 $c$ 点的电势能
如图甲所示, 质量为 $0.2 \mathrm{~kg}$ 的小球套在坚直固定的光滑圆环上,并在圆环最高点保持静止。受到轻微扰动后, 小球由禁止开始沿着圆环运动, 一段时间后, 小球与圆心的连线转过 $\theta$ 角度时, 小球的速度大小为 $v, v^2$ 与 $\cos \theta$ 的关系如图乙所示, $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$. 则
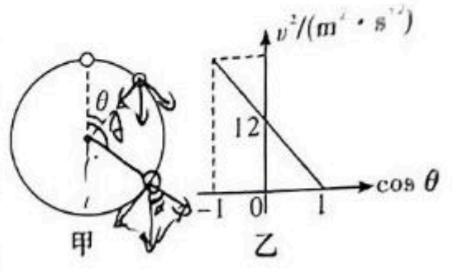
$\text{A.}$ 圆环半径为 $0.6 \mathrm{~m}$
$\text{B.}$ $\theta=\frac{\pi}{2}$ 时, 小球所受合力为 $4 \mathrm{~N}$
$\text{C.}$ $0 \leqslant \theta \leqslant \pi$ 过程中, 圆环对小球的作用力一直增大
$\text{D.}$ $0 \leqslant \theta \leqslant \pi$ 过程中圆环对小球的作用力先减小后增大
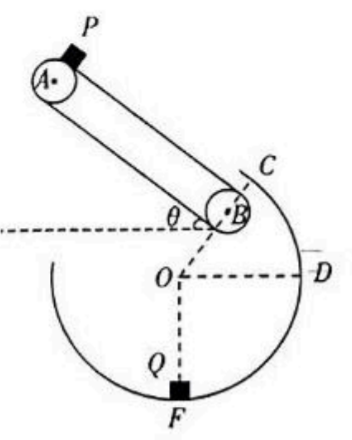
如图所示, 在竖直平面内有一倾角 $\theta=37^{\circ}$ 的传送带, 两皮带轮 $A B$ 轴心之间的距离 $I=3.2 \mathrm{~m}$, 沿顺时针方向以 $v=2 \mathrm{~m} / \mathrm{s}$ 匀速运动, 一质量 $m$ $=2 \mathrm{~kg}$ 的物块 $P$ 从传送带顶端无初速度释放,物块与传送带间的动摩擦因数 $\mu=0.5$ 。物块 $P$ 离开传送带后在 $C$ 点沿切线方向无能量损失地进人半径为 $\frac{5}{9} \mathrm{~m}$ 的光滑圆弧形轨道 $C D F$, 并与位于圆弧轨道最低点 $F$ 的物块 $Q$ 发生碰撞, 碰撞时间极短, 物块 $Q$ 的质量 $M=1 \mathrm{~kg}$, 物块 $P$和 $Q$ 均可视为质点, 重力加速度 $g=10 \mathrm{~m} / \mathrm{s}^2, \sin 37^{\circ}=0.6, \cos 37^{\circ}=0.8$ 。则
$\text{A.}$ 物块 $P$ 到达 $C$ 点时的速度一定为 $4 \mathrm{~m} / \mathrm{s}$
$\text{B.}$ 物块 $P$ 从释放到下滑到 $C$ 点的过程中系统增加的内能为 $9.6 \mathrm{~J}$
$\text{C.}$ 物块 $P$ 与物块 $Q$ 第一次发生碰撞后的瞬间,物块 $P$ 的速度可能为 $1.5 \mathrm{~m} / \mathrm{s}$
$\text{D.}$ 物块 $P$ 与物块 $Q$ 第一次发生碰撞后的瞬间,物块 $P$ 对轨道的压力大小可能为 $35 \mathrm{~N}$
填空题 (共 2 题 ),请把答案直接填写在答题纸上
某同学用如图甲所示的装置探究物体做圆周运动的向心力大小与半径、线速度、质量的关系。用一根细线系住钢球, 另一端连接在固定于铁架台上端的力传感器上, 直径为 $d$ 的钢球静止于 $A$ 点, 将光电门固定在 $A$ 的正下方。钢球底部竖直地粘住一片宽度为 $x$ 的遮光条。
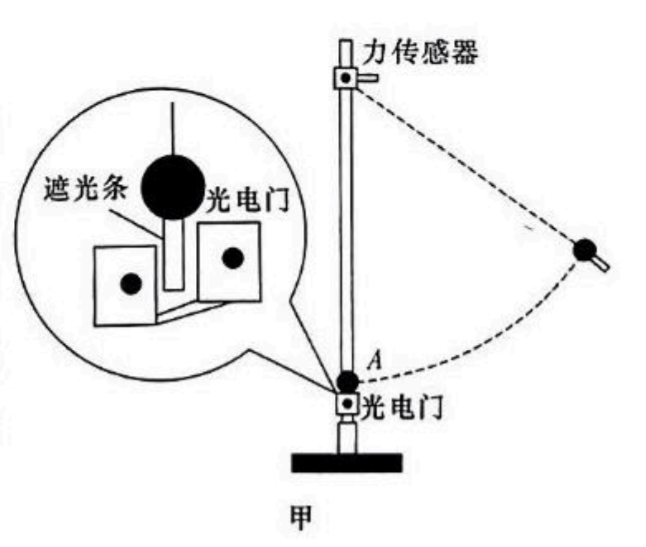
(1) 用天平测出钢球质量, 用刻度尺测出摆线长度。
(2) 将钢球拉至不同位置由静止释放, 读出钢球经过 $A$ 点时力传感器的读数 $F$ 及光电门的遮光时间 $t$, 算出钢球速度的平方值, 具体数据如下表所示:

画出 $F-v^2$ 的关系图像如图乙所示:
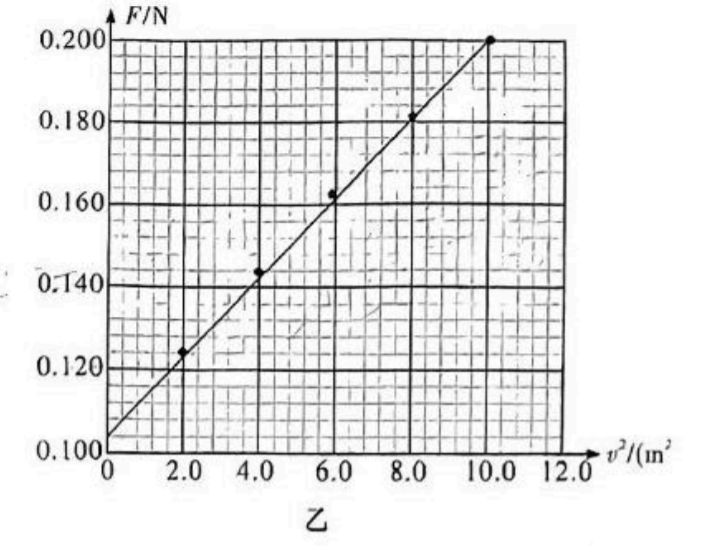
(3)由图像可知,钢球的重力为 ________ $N$ (结果保留 3 位小数)。
(4) 若图像的斜率为 $k$, 钢球质量为 $m$, 重力加速度为 $g$, 则 $F$ 与 $v^2$ 的关系式为 ________ (用所给物理量的符号表示)。
(5)某同学通过进一步学习知道了向心力的公式, 发现实验中使用公式 $m \frac{v^2}{r}$ 求得钢球经过 $A$点的向心力比测量得到的向心力大, 你认为产生误差的主要原因是 ________
A. 钢球运动过程中受到空气阻力的影响
B. 钢球经过光电门的时间过长
C. 光电门测出的是遮光条通过时的速度, 大于钢球球心通过最低点的速度
D. 钢球释放的初始位置细绳与坚直方向夹角大于 $10^{\circ}$
小梦同学自制了一个两挡位 (“ $\times 1$ ”“ $\times 10$ ”) 的欧姆表, 其内部结构如图所示。电流计 $\left(\right.$ ) 的内阻 $R_{\mathrm{G}}=200 \Omega$, 满偏电流 $I_{\mathrm{G}}$ $=15 \mathrm{~mA}$ 。电源电动势 $E=6 \mathrm{~V}$, 内阻 $r=0.5 \Omega$ 。 $R_0$ 为调零电阻, $R_1$ 和 $R_2$ 为定值电阻, “(1)”、“(2)” 为两接线柱。单刀双郑开关 $S$ 与 $m$ 接通时, 欧姆表挡位为 “ $\times 1$ ”, 此时经欧姆调零后, 欧姆表内阻为 $20 \Omega$ 。用此表测量一待测电阻的阻值, 回答下列问题:
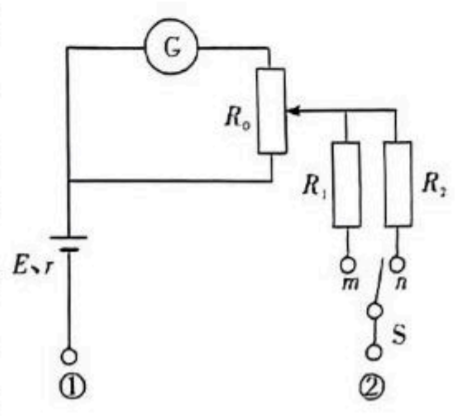
(1) 小梦选择“ $\times 10$ ”挡对 $R_x$ 进行测量。测量前, 先短接、欧姆调零, 短接时红表笔接接线柱(1)。调零后发现 $R_0$ 的滑片指向最上端。则调零电阻的最大阻值 $R_0=$ ________
$\Omega$, 定值电阻 $R_2=$ ________ $\Omega$ 。
(2)选用“×10”挡测量时, 指针偏转过大, 说明待测电阻阻值较小.为使测量更加准确, 应换用小倍率重新测量。小梦选择“ $\times 1$ ”挡重新测量, 测量前, 先短接、欧姆调零. 调零后调零电阻中与电流计(G)串联的部分的阻值为 ________ $\Omega$ 。
(3) 选用 “ $\times 1$ ”挡测量时, 电流表偏转 $\frac{1}{3}$, 则待测电阻 $R_x=$ ________ $\Omega$ 。
(4) 自制欧姆表用了一段时间后, 电源内阻 $r$ 略微增大了一些, 选用 “ $\times 1$ ”挡测量电阻时, 测量值 ________ 真实值。 (填写大于,等于或小于)
解答题 (共 3 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
如图甲所示, 长为 $L 、$ 板间距离也为 $L$ 的平行金属板水平固定放置, 两板间加有如图乙所示的交流电压, 图中 $U_0$ 未知、 $T$ 已知, 在两板中线左端 $P$ 点有一个粒子源, 不断地从 $P$ 点沿两板中线向右均匀地射出质量为 $m$ 、电荷量为 $q$ 的带正电粒子, 粒子穿过两板所用的时间为 $T$, 从 $t=0$ 时刻射入两板间的粒子刚好从下板右端边缘射出, 在两板右侧坚直虚线 $M N$的右侧有坚直向下的匀强电场, 电场中有一长为 $L 、$ 水平放置的荧光屏,荧光屏的上表面与平板下板的上表面在同一水平面上,荧光屏的左端离 $M N$ 的距离为 $\frac{1}{2} L$, 在 $t=0.25 T$ 时刻射出的粒子最终恰好打在荧光屏的中点, 不计粒子重力, 不计粒子间的相互作用, 求:
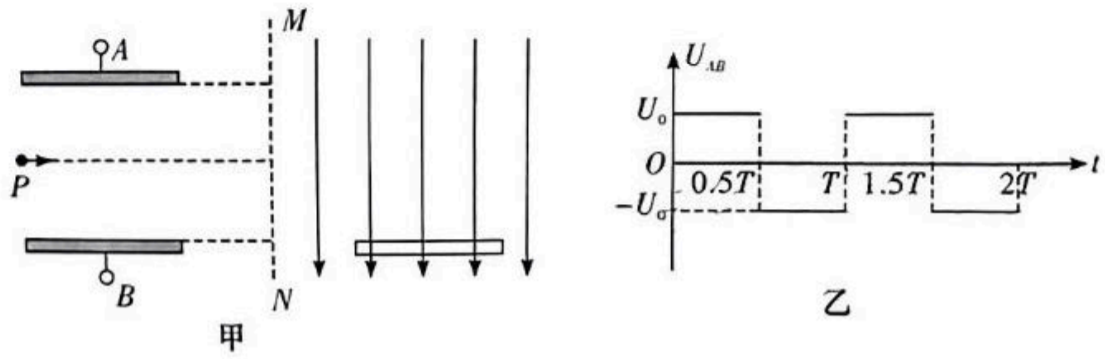
(1) 粒子从 $P$ 点射出的初速度 $v_0$ 大小及两板间电压 $U_0$ 的大小;
(2) 竖直虚线 $M N$ 右侧匀强电场的场强 $E$ 大小;
(3) 屏上能接收到的粒子从两极板间射出时的位置范围。
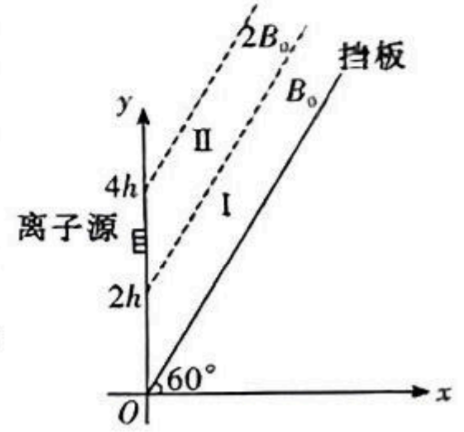
如图所示, 在 $x O y$ 平面的第一象限内有一过原点的无限长挡板, 挡板与 $x$ 轴成 $60^{\circ}$ 角放置。挡板上方有无限长、边界平行于挡板的区域 I 和 II, 分别存在磁感应强度大小为 $B_0$ 和 $2 B_0$ 的匀强磁场,方向均垂直纸面向里, 磁场边界与 $y$ 轴分别交于 $y=2 h$ 和 $y=4 h$ 处。在 $y=3 h$ 处有一离子源射出平行 $x$ 轴、方向与 $x$ 轴正向相同、质量为 $m$ 、电荷量为 $q$ 的正离子。不计正离子的重力以及离子间的相互作用, 并忽略磁场的边缘效应。
(1) 若没有离子进人区域 $I$, 求离子初速度最大值 $v_1$;
(2) 若离子经磁场偏转后垂直 $y$ 轴离开第一象限, 求离子初速度的最大值 $v_2$;
(3) 若离子经磁场偏转后恰好能打到挡板上, 求离子初速度 $v_3$ 。
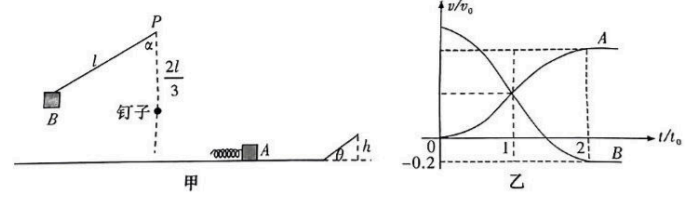
如图甲, 一质量为 $2 m$ 的物块 $B$ (可视为质点) 用一长度为 $l=\frac{v_0^2}{g}$ 的轻绳悬挂于 $P$ 点处 ( $P$ 点与水平面相距 $l$ ), 初始时其与坚直方向的夹角 $\alpha=60^{\circ}, P$ 点正下方 $\frac{2}{3} l$ 处有一钉子。另一物块 $A$ (可视为质点) 与轻质弹簧连接, 静止于光滑水平面上。现自由释放物块 $B$, 当其运动至 $P$ 点正下方时轻绳在钉子的作用下断裂。之后物块 $B$ 将在光滑水平面上匀速直线运动, 直至与物块 $A$ 发生碰撞 (假定在物块 $B$ 触地过程中机械能没有损失, 轻绳在断裂后不影响物块 $B$ 的后续运动)。记物块 $B$ 第一次与弹簧接触的时刻为 $t=0$, 第一次与弹簧分离的时刻为 $t=2 t_0$ 。第一次碰撞过程中, $A 、 B$ 的 $v-t$ 图像如图乙所示。已知从 $t=0$ 到 $t=t_0$ 时间内, 物块 $A$ 运动的距离为 $0.144 v_0 t_0 。 A 、 B$ 分离后, $A$ 滑上粗糙斜面, 然后滑下, 与一直在水平面上运动的 $B$ 再次碰撞。斜面倾角 $\theta=37^{\circ}$, 高度 $h=\frac{v_0^2}{5 g}$, 与水平面光滑连接。已知碰撞过程中弹簧始终处于弹性限度内, 重力加速度为 $g, \sin \theta=0.6$ 。求:
(1) 轻绳即将断裂时的张力;
(2)第一次碰撞过程中, 弹簧压缩量的最大值 $\Delta x$ (用 $v_0 、 t_0$ 表示);
(3) 物块 $A$ 与斜面间的动摩擦因数 $\mu$ 的取值范围。