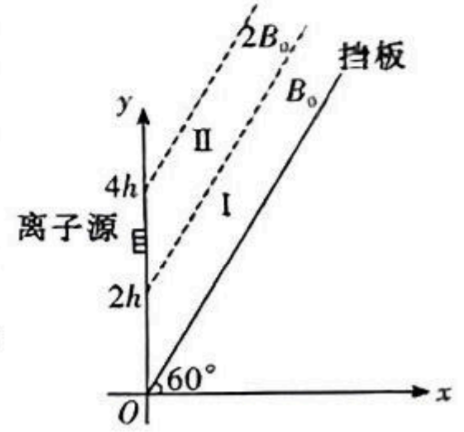
如图所示, 在 $x O y$ 平面的第一象限内有一过原点的无限长挡板, 挡板与 $x$ 轴成 $60^{\circ}$ 角放置。挡板上方有无限长、边界平行于挡板的区域 I 和 II, 分别存在磁感应强度大小为 $B_0$ 和 $2 B_0$ 的匀强磁场,方向均垂直纸面向里, 磁场边界与 $y$ 轴分别交于 $y=2 h$ 和 $y=4 h$ 处。在 $y=3 h$ 处有一离子源射出平行 $x$ 轴、方向与 $x$ 轴正向相同、质量为 $m$ 、电荷量为 $q$ 的正离子。不计正离子的重力以及离子间的相互作用, 并忽略磁场的边缘效应。
(1) 若没有离子进人区域 $I$, 求离子初速度最大值 $v_1$;
(2) 若离子经磁场偏转后垂直 $y$ 轴离开第一象限, 求离子初速度的最大值 $v_2$;
(3) 若离子经磁场偏转后恰好能打到挡板上, 求离子初速度 $v_3$ 。