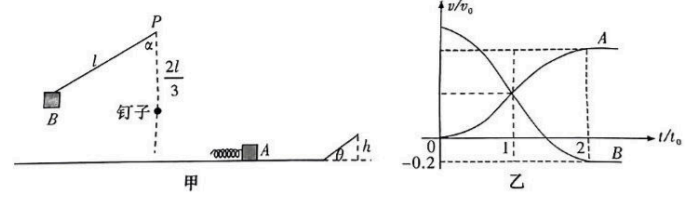
如图甲, 一质量为 $2 m$ 的物块 $B$ (可视为质点) 用一长度为 $l=\frac{v_0^2}{g}$ 的轻绳悬挂于 $P$ 点处 ( $P$ 点与水平面相距 $l$ ), 初始时其与坚直方向的夹角 $\alpha=60^{\circ}, P$ 点正下方 $\frac{2}{3} l$ 处有一钉子。另一物块 $A$ (可视为质点) 与轻质弹簧连接, 静止于光滑水平面上。现自由释放物块 $B$, 当其运动至 $P$ 点正下方时轻绳在钉子的作用下断裂。之后物块 $B$ 将在光滑水平面上匀速直线运动, 直至与物块 $A$ 发生碰撞 (假定在物块 $B$ 触地过程中机械能没有损失, 轻绳在断裂后不影响物块 $B$ 的后续运动)。记物块 $B$ 第一次与弹簧接触的时刻为 $t=0$, 第一次与弹簧分离的时刻为 $t=2 t_0$ 。第一次碰撞过程中, $A 、 B$ 的 $v-t$ 图像如图乙所示。已知从 $t=0$ 到 $t=t_0$ 时间内, 物块 $A$ 运动的距离为 $0.144 v_0 t_0 。 A 、 B$ 分离后, $A$ 滑上粗糙斜面, 然后滑下, 与一直在水平面上运动的 $B$ 再次碰撞。斜面倾角 $\theta=37^{\circ}$, 高度 $h=\frac{v_0^2}{5 g}$, 与水平面光滑连接。已知碰撞过程中弹簧始终处于弹性限度内, 重力加速度为 $g, \sin \theta=0.6$ 。求:
(1) 轻绳即将断裂时的张力;
(2)第一次碰撞过程中, 弹簧压缩量的最大值 $\Delta x$ (用 $v_0 、 t_0$ 表示);
(3) 物块 $A$ 与斜面间的动摩擦因数 $\mu$ 的取值范围。
(1) 轻绳即将断裂时的张力;
(2)第一次碰撞过程中, 弹簧压缩量的最大值 $\Delta x$ (用 $v_0 、 t_0$ 表示);
(3) 物块 $A$ 与斜面间的动摩擦因数 $\mu$ 的取值范围。
