如图所示, 在竖直平面内有一倾角 $\theta=37^{\circ}$ 的传送带, 两皮带轮 $A B$ 轴心之间的距离 $I=3.2 \mathrm{~m}$, 沿顺时针方向以 $v=2 \mathrm{~m} / \mathrm{s}$ 匀速运动, 一质量 $m$ $=2 \mathrm{~kg}$ 的物块 $P$ 从传送带顶端无初速度释放,物块与传送带间的动摩擦因数 $\mu=0.5$ 。物块 $P$ 离开传送带后在 $C$ 点沿切线方向无能量损失地进人半径为 $\frac{5}{9} \mathrm{~m}$ 的光滑圆弧形轨道 $C D F$, 并与位于圆弧轨道最低点 $F$ 的物块 $Q$ 发生碰撞, 碰撞时间极短, 物块 $Q$ 的质量 $M=1 \mathrm{~kg}$, 物块 $P$和 $Q$ 均可视为质点, 重力加速度 $g=10 \mathrm{~m} / \mathrm{s}^2, \sin 37^{\circ}=0.6, \cos 37^{\circ}=0.8$ 。则
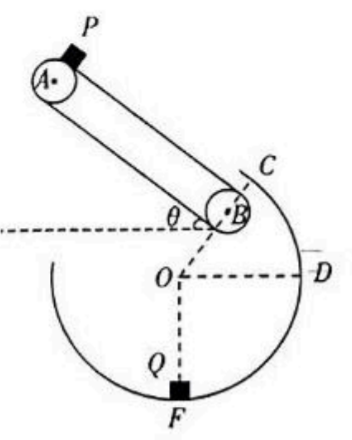

A. 物块 $P$ 到达 $C$ 点时的速度一定为 $4 \mathrm{~m} / \mathrm{s}$
B. 物块 $P$ 从释放到下滑到 $C$ 点的过程中系统增加的内能为 $9.6 \mathrm{~J}$
C. 物块 $P$ 与物块 $Q$ 第一次发生碰撞后的瞬间,物块 $P$ 的速度可能为 $1.5 \mathrm{~m} / \mathrm{s}$
D. 物块 $P$ 与物块 $Q$ 第一次发生碰撞后的瞬间,物块 $P$ 对轨道的压力大小可能为 $35 \mathrm{~N}$