查看原题
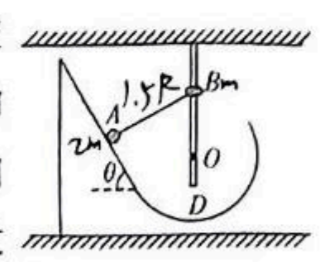
如图所示, 固定光滑斜面倾角 θ=60∘, 其底端与竖直面内半径为 R 的固定光滑圆弧轨道相切, 位置 D 为圆弧轨道的最低点。质量为 2m 的小球 A 和质量为 m 的小环 B (均可视为质点) 用 L=1.5R 的轻杆通过轻质较链相连。 B 套在光滑的固定竖直长杆上, 杆和圆轨道在同一坚直平面内, 杆过轨道圆心 O, 初始轻杆与斜面垂直。在斜面上由静止释放 A, 假设在运动过程中两杆不会碰撞, 小球能滑过 D 点且通过轨道连接处时无能量损失 (速度大小不变), 重力加速度为 g, 从小球 A 由静止释放到运动至最低点的过程中, 下列判断正确的是
A. A 和 B 组成的系统的机械能不守恒     B. 刚释放时小球 A 的加速度大小为 32g     C. 小环 B 速度最大时轻杆弹力为 mg     D. 小球 A 运动到最低点时的速度大小为 3gR3         
不再提醒