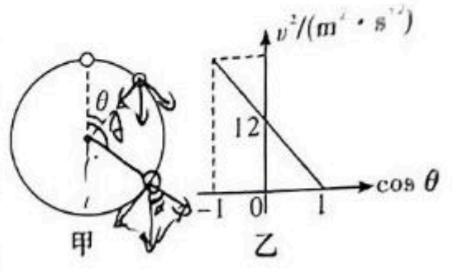
如图甲所示, 质量为 $0.2 \mathrm{~kg}$ 的小球套在坚直固定的光滑圆环上,并在圆环最高点保持静止。受到轻微扰动后, 小球由禁止开始沿着圆环运动, 一段时间后, 小球与圆心的连线转过 $\theta$ 角度时, 小球的速度大小为 $v, v^2$ 与 $\cos \theta$ 的关系如图乙所示, $g$ 取 $10 \mathrm{~m} / \mathrm{s}^2$. 则
A
圆环半径为 $0.6 \mathrm{~m}$
B
$\theta=\frac{\pi}{2}$ 时, 小球所受合力为 $4 \mathrm{~N}$
C
$0 \leqslant \theta \leqslant \pi$ 过程中, 圆环对小球的作用力一直增大
D
$0 \leqslant \theta \leqslant \pi$ 过程中圆环对小球的作用力先减小后增大
E
F