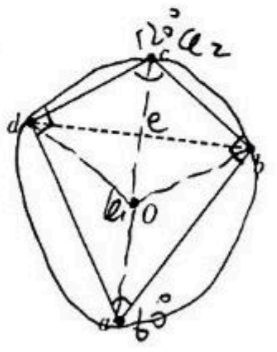
如图所示, 四边形 $a b c d$ 中, $a b=a d, c d=c b, a d$ 垂直 $d c 、 a b$ 垂直 $b c, \angle c=$ $120^{\circ}, O$ 点和 $c$ 点关于直线 $b d$ 对称, $O c$ 连线与 $d b$ 连线的交点为 $e$ (未标出)。在 $a, b$ 和 $d$ 点各固定一个带电荷量为 $q$ 的正电荷, $O$ 点和 $c$ 点的电势分别为 $\varphi_1$ 和 $\varphi_2$ 。下列说法正确的是
A
$c$ 点的电场强度方向由 $O$ 指向 $c$, 且小于 $e$ 点的电场强度大小
B
若仅将 $a$ 点的正电荷换成带相同电荷量的负电荷, 则 $c$ 点电势等于 $\frac{4}{3} \varphi_1-\varphi_2$
C
若仅将 $b$ 点的正电荷换成带相同电荷量的负电荷, 则 $c$ 点电势等于 $\varphi_2-\frac{1}{2} \varphi_1$
D
电子在 $O$ 点的电势能小于在 $c$ 点的电势能
E
F