2021年浙江省温州市中考数学试卷

导出试卷

2021年浙江省温州市中考数学试卷

一、单选题（共 8 题），每题只有一个选项正确

1. 计算

(- 2)^{2}

的结果是（　　）

A.

4

B.

- 4

C.

1

D.

- 1

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

2. 直六棱柱如图所示，它的俯视图是（　　）

A.

B.

C.

D.

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

3. 第七次全国人口普查结果显示，我国具有大学文化程度的人口超218000000人．数据218000000用科学记数法表示为（　　）

A.

218 \times 10^{6}

B.

21.8 \times 10^{7}

C.

2.18 \times 10^{8}

D.

0.218 \times 10^{9}

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4. 如图是某天参观温州数学名人馆的学生人数统计图．若大学生有60人，则初中生有

A.

45

B.

75

C.

120

D.

300

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

5. 解方程

- 2 (2 x + 1) = x

，以下去括号正确的是（　　）

A.

- 4 x + 1 = - x

B.

- 4 x + 2 = - x

C.

- 4 x - 1 = - x

D.

- 4 x - 2 = - x

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

6. 如图，图形甲与图形乙是位似图形，

O

是位似中心，位似比为

2 : 3

，点

A, B

的对应点分别为点

A^{'}, B^{'}

, 若

A B = 6

，则

A^{'} B^{'}

的长为（　　）

A.

8

B.

9

C.

10

D.

15

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

7. 某地居民生活用水收费标准：每月用水量不超过17立方米，每立方米

a

元；超过部分每立方米

(a + 1.2)

元．该地区某用户上月用水量为20立方米，则应缴水费为（　　）

A.

20 a

元

B.

(20 a + 24)

元

C.

(17 a + 3.6)

元

D.

(20 a + 3.6)

元

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

8. 图1是第七届国际数学教育大会(ICME) 会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图2所示的四边形OABC ．若

A B = B C = 1, ∠ A O B = α

，则

O C^{2}

的值为（　　）

A.

\frac{1}{\sin^{2} α} + 1

B.

\sin^{2} α + 1

C.

\frac{1}{\cos^{2} α} + 1

D.

\cos^{2} α + 1

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

二、填空题（共 6 题），请把答案直接填写在答题纸上

9. 分解因式：

2 m^{2} - 18 =

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

10. 一个不透明的袋中装有21个只有颜色不同的球，其中5个红球，7个白球，9个黄球．从中任意摸出1个球是红球的概率为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

11. 若扇形的圆心角为

30^{0}

，半径为17，则扇形的弧长为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

12. 不等式组

{\begin{cases} x - 3 < 4 \\ \frac{3 x + 2}{5} > 1 \end{cases}

的解集为

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

13. 如图，圆

O

与

△ A B C

的边

B

相切，切点为B,

△ A B C

将绕点B 按顺时针方向旋转得到

△ O^{'} A^{'} B

，使点

O^{'}

落在圆O上，边A'B 交线段AO于点C 若

∠ a^{'} = 25^{0}

，则

∠ O C B

= （　　）度．

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

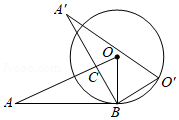
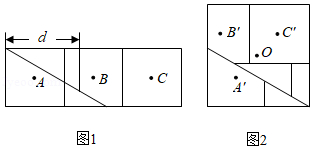
14. 图1是邻边长为

2

和

6

的矩形，它由三个小正方形组成，将其剪拼成不重叠、无缝隙的大正方形（如图2) ，则图1中所标注的d的值为（　　）；记图1中小正方形的中心为点

A, B, C

图2中的对应点为点

A^{'}, B^{'} C,

．以大正方形的中心

O

为圆心作圆，则当点

A^{'}, B^{'}, C^{'}

在圆内或圆上时，圆的最小面积为（　　）

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

三、解答题（共 10 题），解答过程应写出必要的文字说明、证明过程或演算步骤

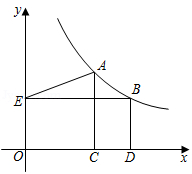
15. 如图，点

A, B

在反比例函数

y = \frac{k}{x} (k > 0, x > 0)

的图象上，

A C ⊥ x

轴于点

C

，

B D ⊥ x

轴于点

D

，

B E ⊥ y

轴于点

E

，连结

A E

．若

O E = 1

O C = \frac{2}{3} O D

A C = A E

,则

k

的值为（　　）

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

16. 由四个全等的直角三角形和一个小正方形组成的大正方形

A B C D

如图所示．过点D作DF的垂线交小正方形对角线的延长线于点G ，连结CG ，延长BE 交CG 于点H ．若

A E = 2 B E

，则

\frac{C G}{B H}

的值为（　　）

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

17. 计算
(1)

4 \times (- 3) + | - 8 | - \sqrt{9} + (\sqrt{7})^{0}

(2)化简

(a - 5)^{2} + \frac{1}{2} a (2 a + 8)

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

18. 如图BE 是

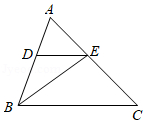
△ A B C

的角平分线，在AB上取点D，使

D B = D E

，
（1）求证：

D E / / B C

(2) 若

∠ A = 65^{\circ}, ∠ A E D = 45^{\circ}

,求

∠ E B C

的度数。

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

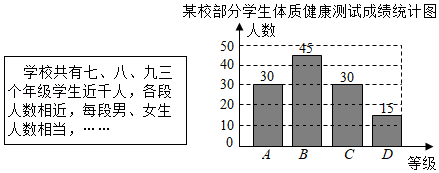
19. 某校将学生体质健康测试成绩分为A ，B ，C ，D 四个等级，依次记为4分，3分，2分，1分．为了解学生整体体质健康状况，拟抽样进行统计分析．
（1）以下是两位同学关于抽样方案的对话：
小红：“我想随机抽取七年级男、女生各60人的成绩．”
小明：“我想随机抽取七、八、九年级男生各40人的成绩．”
根据如图学校信息，请你简要评价小红、小明的抽样方案．
如果你来抽取120名学生的测试成绩，请给出抽样方案．
（2）现将随机抽取的测试成绩整理并绘制成如图统计图，请求出这组数据的平均数、中位数和众数．

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

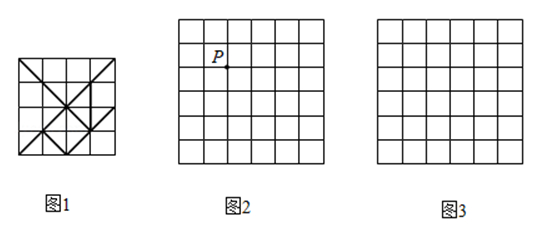
20. 如图中

4 \times 4

与

6 \times 6

的方格都是由边长为1的小正方形组成．图1是绘成的七巧板图案，它由7个图形组成，请按以下要求选择其中一个并在图2、图3中画出相应的格点图形（顶点均在格点上）．
（1）选一个四边形画在图2中，使点为它的一个顶点，并画出将它向右平移3个单位后所得的图形．
（2）选一个合适的三角形，将它的各边长扩大到原来的

\sqrt{5}

倍，画在图3中．

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

21. 已知抛物线

y = a x^{2} - 2 a x - 8 (a \neq 0)

经过点

(- 2, 0)

．
（1）求抛物线的函数表达式和顶点坐标．
（2）直线

l

交抛物线于点

A (- 4, M), B (N, 7)

, n为正数．若点

P

在抛物线上且在直线

l

下方（不与点

A ， B

重合），分别求出点P横坐标与纵坐标的取值范围．

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

22.

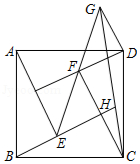
▱ A B C D

中

E ， F

是对角线

B D

上的两点（点E 在点F 左侧），且

△ A E B = △ C F D = 90^{\circ}

（1）求证：四边形AECF是平行四边形；
（2）当

A B = 5, t a n ∠ A B E = \frac{3}{4} ， ∠ C B E = ∠ E A F

时，求

B D

的长．

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

23. 某公司生产的一种营养品信息如表．已知甲食材每千克的进价是乙食材的2倍，用80元购买的甲食材比用20元购买的乙食材多1千克．

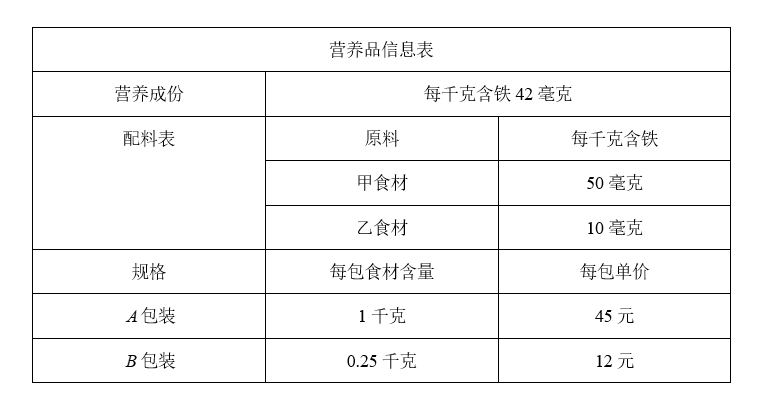
（1）问甲、乙两种食材每千克进价分别是多少元？
（2）该公司每日用18000元购进甲、乙两种食材并恰好全部用完．
①问每日购进甲、乙两种食材各多少千克？
②已知每日其他费用为2000元，且生产的营养品当日全部售出．若的数量不低于的数量，则为多少包时，每日所获总利润最大？最大总利润为多少元？

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

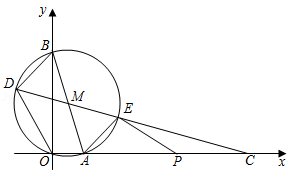
24. 如图，在平面直角坐标系中，圆M经过原点O ，分别交x轴、 y轴于点

A (2, 0), B (0, 8)

连结AB ．直线CM 分别交圆M于点D ，E（点D 在左侧），交x 轴于点

C (17, 0)

，连结AE
（1）求圆M的半径和直线CM的函数表达式；
（2）求点D ，E的坐标；
（3）点P在线段AC上，连结PE ．当

∠ A E P

与

△ O B D

的一个内角相等时，求所有满足条件的OP的长．

查看分享下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。