广西壮族自治区2023年中考数学试卷

导出试卷

广西壮族自治区2023年中考数学试卷

单选题（共 12 题），每题只有一个选项正确

若零下 5 摄氏度记为 $-5^{\circ} \mathrm{C}$, 则零上 5 摄氏度记为

$\text{A.}$ $-5^{\circ} \mathrm{C}$ $\text{B.}$ $0^{\circ} \mathrm{C}$ $\text{C.}$ $+5^{\circ} \mathrm{C}$ $\text{D.}$ $+4^{\circ} \mathrm{C}$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

下列数学经典图形中, 是中心对称图形的是

$\text{A.}$

$\text{B.}$

$\text{C.}$

$\text{D.}$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

若分式 $\frac{1}{x+1}$ 有意义, 则 $\mathrm{x}$ 的取值范围是

$\text{A.}$ $x \neq-1$ $\text{B.}$ $x \neq 0$ $\text{C.}$ $x \neq 1$ $\text{D.}$ $x \neq 2$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 点 $\mathrm{A} 、 \mathrm{~B} 、 \mathrm{C}$ 在 $\odot O$ 上, $\angle C=40^{\circ}$, 则 $\angle A O B$ 的度数是

$\text{A.}$ $50^{\circ}$ $\text{B.}$ $60^{\circ}$ $\text{C.}$ $70^{\circ}$ $\text{D.}$ $80^{\circ}$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

$x \leq 2$ 在数轴上表示正确的是

$\text{A.}$

$\text{B.}$

$\text{C.}$

$\text{D.}$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

甲、乙、丙、丁四名同学参加立定跳远训练, 他们成绩的平均数相同, 方差如下: $S_{\text {甲 }}^2=2.1, S_Z^2=3.5$, $S_{\text {丙 }}^2=9, S_T^2=0.7$, 则成绩最稳定的是

$\text{A.}$ 甲 $\text{B.}$ 乙 $\text{C.}$ 丙 $\text{D.}$ 丁

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 一条公路两次转弯后又回到与原来相同的方向, 如果 $\angle A=130^{\circ}$, 那么 $\angle B$ 的度数是

$\text{A.}$ $160^{\circ}$ $\text{B.}$ $150^{\circ}$ $\text{C.}$ $140^{\circ}$ $\text{D.}$ $130^{\circ}$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

下列计算正确的是

$\text{A.}$ $a^3+a^4=a^7$ $\text{B.}$ $a^3 \cdot a^4=a^7$ $\text{C.}$ $a^4 \div a^3=a^7$ $\text{D.}$ $\left(a^3\right)^4=a^7$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

将抛物线 $y=x^2$ 向右平移 3 个单位, 再向上平移 4 个单位, 得到的抛物线是

$\text{A.}$ $y=(x-3)^2+4$ $\text{B.}$ $y=(x+3)^2+4$ $\text{C.}$ $y=(x+3)^2-4$ $\text{D.}$ $y=(x-3)^2-4$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

赵州桥是当今世界上建造最早, 保存最完整的中国古代单孔敞肩石拱桥. 如图, 主桥拱呈圆弧形, 跨度约为 $37 \mathrm{~m}$, 拱高约为 $7 \mathrm{~m}$, 则赵州桥主桥拱半径 $\mathrm{R}$ 约为

$\text{A.}$ $20 \mathrm{~m}$ $\text{B.}$ $18 \mathrm{~m}$ $\text{C.}$ $35 \mathrm{~m}$ $\text{D.}$ $40 \mathrm{~m}$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

据国家统计局发布的《2022 年国民经济和社会发展统计公报》显示, 2020 年和 2022 年全国居民人均可支配收入分别为 3.2 万元和 3.7 万元. 设 2020 年至 2022 年全国居民人均可支配收入的年平均增长率为 $x$,依题意可列方程为

$\text{A.}$ $3.2(1-x)^2=3.7$ $\text{B.}$ $3.2(1+x)^2=3.7$ $\text{C.}$ $3.7(1-x)^2=3.2$ $\text{D.}$ $3.7(1+x)^2=3.2$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 过 $y=\frac{k}{x}(x>0)$ 的图象上点 $\mathrm{A}$, 分别作 $\mathrm{x}$ 轴, $\mathrm{y}$ 轴的平行线交 $y=-\frac{1}{x}$ 的图象于 $\mathrm{B}, \mathrm{D}$ 两点, 以 $A B$, $A D$ 为邻边的矩形 $A B C D$ 被坐标轴分割成四个小矩形, 面积分别记为 $S_1, S_2, S_3, S_4$, 若 $S_2+S_3+S_4=\frac{5}{2}$,则 $k$ 的值为

$\text{A.}$ 4 $\text{B.}$ 3 $\text{C.}$ 2 $\text{D.}$ 1

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

填空题（共 6 题），请把答案直接填写在答题纸上

化简: $\sqrt{9}=$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

分解因式: $a^2+5 a=$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

函数 $y=k x+3$ 的图象经过点 $(2,5)$, 则 $k=$

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

某班开展“梦想未来、青春有我”主题班会, 第一小组有 2 位男同学和 3 位女同学, 现从中随机抽取 1 位同学分享个人感悟, 则抽到男同学的概率是

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 焊接一个钢架, 包括底角为 $37^{\circ}$ 的等腰三角形外框和 $3 \mathrm{~m}$ 高的支柱, 则共需钢材约 $\mathrm{m}($ 结果取整数). (参考数据: $\sin 37^{\circ} \approx 0.60, \cos 37^{\circ} \approx 0.80, \tan 37^{\circ} \approx 0.75$ )

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 在边长为 2 的正方形 $A B C D$ 中, $\mathrm{E}, \mathrm{F}$ 分别是 $B C, C D$ 上的动点, $\mathrm{M}, \mathrm{N}$ 分别是 $E F, A F$ 的中点,则 $M N$ 的最大值为

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

解答题（共 8 题），解答过程应写出必要的文字说明、证明过程或演算步骤

计算: $(-1) \times(-4)+2^2 \div(7-5)$.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

解分式方程: $\frac{2}{x-1}=\frac{1}{x}$.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, 在 $\triangle A B C$ 中, $\angle A=30^{\circ}, \angle B=90^{\circ}$.
(1) 在斜边 $A C$ 上求作线段 $A O$, 使 $A O=B C$, 连接 $O B$;
(要求: 尺规作图并保留作图痕迹, 不写作法, 标明字母)
(2) 若 $O B=2$, 求 $A B$ 的长.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

4 月 24 日是中国航天日，为激发青少年崇尚科学、探索未知的热情，航阳中学开展了“航空航天”知识问答系列活动.为了解活动效果，从七、八年级学生的知识问答成绩中，各随机抽取 20 名学生的成绩进行统计分析（6 分及 6 分以上为合格），数据整理如下：

(1) 写出统计表中 $\mathrm{a}, \mathrm{b}, \mathrm{c}$ 的值;
(2) 若该校八年级有 600 名学生, 请估计该校八年级学生成绩合格的人数;
（3）从中位数和众数中任选其一, 说明其在本题中的实际意义.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, $P O$ 平分 $\angle A P D, P A$ 与 $\odot O$ 相切于点 $\mathrm{A}$, 延长 $A O$ 交 $P D$ 于点 $\mathrm{C}$, 过点 $\mathrm{O}$ 作 $O B \perp P D$, 垂足为 $\mathrm{B}$.
(1) 求证: $P B$ 是 $\odot O$ 的切线;
(2) 若 $\odot O$ 的半径为 $4, O C=5$, 求 $P A$ 的长.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

如图, $\triangle A B C$ 是边长为 4 的等边三角形, 点 $\mathrm{D}, \mathrm{E}, \mathrm{F}$ 分别在边 $A B, B C, C A$ 上运动, 满足 $A D=B E=C F$.
(1) 求证: $\triangle A D F \cong \triangle B E D$;
(2) 设 $A D$ 的长为 $\mathrm{x}, \triangle D E F$ 的面积为 $\mathrm{y}$, 求 $\mathrm{y}$ 关于 $\mathrm{x}$ 的函数解析式;
(3) 结合 (2) 所得的函数, 描述 $\triangle D E F$ 的面积随 $A D$ 的增大如何变化.

查看分享编辑下载此题点赞(1) 收藏(0) 错题本(0) 白板加入试卷

有言道: “杆秤一头称起人间生计, 一头称起天地良心”. 某兴趣小组将利用物理学中杜杆原理制作简易杆称.小组先设计方案, 然后动手制作, 再结合实际进行调试, 请完成下列方案设计中的任务.
【知识背景】如图, 称重物时, 移动科砣可使杆秤平衡, 根据杠杆原理推导得: $\left(m_0+m\right) \cdot l=M \cdot(a+y)$.其中秤盘质量 $m_0$ 克, 重物质量 $\mathrm{m}$ 克, 秤砣质量 $\mathrm{M}$ 克, 秤纽与秤盘的水平距离为 1 厘米, 秤纽与零刻线的水平距离为 $\mathrm{a}$ 厘米, 秤砣与零刻线的水平距离为 $\mathrm{y}$ 厘米.

【方案设计】
目标: 设计简易杆秤. 设定 $m_0=10, M=50$, 最大可称重物质量为 1000 克, 零刻线与末刻线的距离定为 50 厘米.

任务一: 确定 $\iota$ 和 $\mathrm{a}$ 的值.
（1）当科盘不放重物, 秤砣在零刻线时, 杆科平衡, 请列出关于 $l, a$ 的方程;
(2) 当科盘放入质量为 1000 克的重物, 秤砣从零刻线移至末刻线时, 杆科平衡, 请列出关于 $l, \mathrm{a}$ 的方程;
(3) 根据 (1) 和 (2) 所列方程, 求出 $\zeta$ 和 $\mathrm{a}$ 的值.

任务二: 确定刻线的位置.
（4）根据任务一, 求 $\mathrm{y}$ 关于 $\mathrm{m}$ 的函数解析式;
(5) 从零刻线开始, 每隔 100 克在秤杆上找到对应刻线, 请写出相邻刻线间的距离.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

【探究与证明】
折纸, 操作简单, 富有数学趣味, 我们可以通过折纸开展数学探究, 探索数学奥秘.
【动手操作】如图 1 , 将矩形纸片 $A B C D$ 对折, 使 $A D$ 与 $B C$ 重合, 展平纸片, 得到折痕 $E F$; 折叠纸片, 使点 $\mathrm{B}$ 落在 $E F$ 上, 并使折痕经过点 $\mathrm{A}$, 得到折痕 $A M$, 点 $\mathrm{B}, \mathrm{E}$ 的对应点分别为 $B^{\prime}, E^{\prime}$, 展平纸片, 连接 $A B^{\prime}$, $B B^{\prime}, B E^{\prime}$.

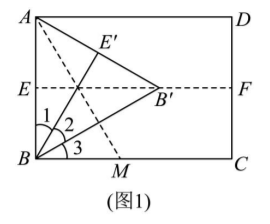
请完成:
(1) 观察图 1 中 $\angle 1, \angle 2$ 和 $\angle 3$, 试猜想这三个角的大小关系;
(2) 证明（1）中的猜想;

【类比操作】如图 2, $\mathrm{N}$ 为矩形纸片 $A B C D$ 的边 $A D$ 上的一点, 连接 $B N$, 在 $A B$ 上取一点 $\mathrm{P}$, 折叠纸片, 使 $\mathrm{B}, \mathrm{P}$ 两点重合, 展平纸片, 得到折痕 $E F$; 折叠纸片, 使点 $\mathrm{B}, \mathrm{P}$ 分别落在 $E F, B N$ 上, 得到折痕 $\mathrm{l}$, 点 $\mathrm{B}$, $\mathrm{P}$ 的对应点分别为 $B^{\prime}, P^{\prime}$, 展平纸片, 连接, $P^{\prime} B^{\prime}$.

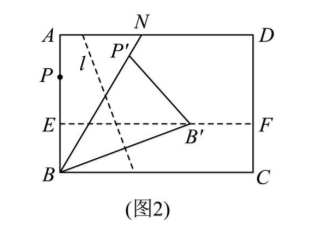
(3) 证明 $B B^{\prime}$ 是 $\angle N B C$ 的一条三等分线.

查看分享编辑下载此题点赞(0) 收藏(0) 错题本(0) 白板加入试卷

非会员每天可以查看15道试题。开通会员，海量试题无限制查看。

无限看试题
下载试题
组卷

开通会员

热点推荐

试卷二维码

分享此二维码到群，让更多朋友参与

试卷白板

试卷白板提供了一个简单的触摸书写板，可供老师上课、或者视频直播时，直接利用白板给学生讲解试题，如有意见，欢迎反馈。