有言道: “杆秤一头称起人间生计, 一头称起天地良心”. 某兴趣小组将利用物理学中杜杆原理制作简易杆称.小组先设计方案, 然后动手制作, 再结合实际进行调试, 请完成下列方案设计中的任务.
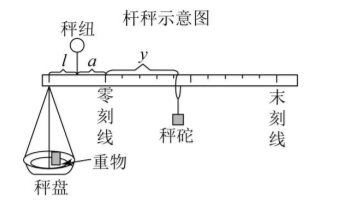
【知识背景】如图, 称重物时, 移动科砣可使杆秤平衡, 根据杠杆原理推导得: $\left(m_0+m\right) \cdot l=M \cdot(a+y)$.其中秤盘质量 $m_0$ 克, 重物质量 $\mathrm{m}$ 克, 秤砣质量 $\mathrm{M}$ 克, 秤纽与秤盘的水平距离为 1 厘米, 秤纽与零刻线的水平距离为 $\mathrm{a}$ 厘米, 秤砣与零刻线的水平距离为 $\mathrm{y}$ 厘米.

【方案设计】
目标: 设计简易杆秤. 设定 $m_0=10, M=50$, 最大可称重物质量为 1000 克, 零刻线与末刻线的距离定为 50 厘米.

任务一: 确定 $\iota$ 和 $\mathrm{a}$ 的值.
（1）当科盘不放重物, 秤砣在零刻线时, 杆科平衡, 请列出关于 $l, a$ 的方程;
(2) 当科盘放入质量为 1000 克的重物, 秤砣从零刻线移至末刻线时, 杆科平衡, 请列出关于 $l, \mathrm{a}$ 的方程;
(3) 根据 (1) 和 (2) 所列方程, 求出 $\zeta$ 和 $\mathrm{a}$ 的值.

任务二: 确定刻线的位置.
（4）根据任务一, 求 $\mathrm{y}$ 关于 $\mathrm{m}$ 的函数解析式;
(5) 从零刻线开始, 每隔 100 克在秤杆上找到对应刻线, 请写出相邻刻线间的距离.