如图, 在 Rt $\triangle A B C$ 中, $A B=A C$, 点 $F$ 为 $A C$ 上一点, 连接 $B F$, 以点 $C$ 为圆心, $C A$ 长 为半径作弧交 $B F$ 于点 $E$, 连接 $A E$. 点 $D$ 为 $B C$ 中点, 连接 $D E$.
(1) 求证: $\angle \mathrm{ACE}=2 \angle \mathrm{BAE}$;
(2) 探究 $\mathrm{BE}$ 与 $\mathrm{DE}$ 的数量关系, 并证明;
(3) 若 $\mathrm{AF}=1, \mathrm{CF}=2$, 求 $\mathrm{EF}$ 的长.

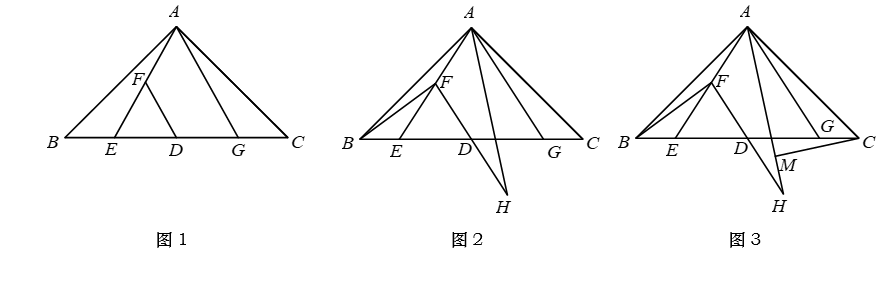
如图 1, 在等腰 Rt $\triangle \mathrm{ABC}$ 中, $\angle \mathrm{BAC}=90^{\circ}$, 点 $\mathrm{D}$ 为 $\mathrm{BC}$ 中点, 点 $\mathrm{E}$ 为 $\mathrm{BC}$ 上一点, 连接 $A E$. 取 $A E$ 中点 $F$, 连接 $D F$. 在 $B C$ 上取 $G$, 使 $B E=C G$, 连接 $A G$.
(1) 探究线段 DF 与 $A G$ 的关系, 并证明;
(2) 如图 2, 延长 $\mathrm{FD}$ 至 $\mathrm{H}$ 使 $\mathrm{FD}=\mathrm{HD}$, 连接 $\mathrm{AH} 、 \mathrm{BF}$. 若 $\angle \mathrm{EAH}=45^{\circ}$, 求证: $\sqrt{2}$ $\mathrm{EF}=\mathrm{BF} ;$
(3) 如图 3, 在 (2) 的条件下, 过 C 作 $\mathrm{CM} \perp \mathrm{AH}$ 于 $\mathrm{M}$. 请直接写出 $\frac{\mathrm{AH}}{\mathrm{HM}}$ 的值.

如图 1, 在 $\triangle A B C$ 中, $A B=A C, C D / / A B$, 点 $E$ 为 $A C$ 中点, 连接 $D E$. 以点 $E$ 为圆心, $D E$ 为半径作弧交 $A B$ 于 $F$. 点 $G$ 在 $A B$ 延长线上, 连接 $G D$. 过 $G$ 作 $G H \perp D E$ 于 $H$, 连 接 $\mathrm{HF}$. 若 $\angle \mathrm{FGD}=45^{\circ}$.
(1) 在图中找出与 $\angle \mathrm{AFE}$ 相等的角, 并证明;
(2) 求 $\angle \mathrm{FHG}$ 的度数;
(3) 如图 2, 当 $\mathrm{BG}=\mathrm{CD}=1, \mathrm{AB}=4$, 求 $\mathrm{EH}$ 的长.

如图 1, 在等腰 Rt $\triangle A B C$ 中, $A B=A C$, 点 $D$ 为 $B C$ 的中点. 点 $F$ 为 $A B$ 边上一点, 连接 $\mathrm{CF}$, 过点 $\mathrm{D}$ 作 $\mathrm{DE} \perp \mathrm{CF}$ 于点 $\mathrm{E}$, 连接 $\mathrm{AE}$.
(1) 探究 $\angle \mathrm{EDC}$ 与 $\angle \mathrm{AFC}$ 间的数量关系, 并证明;
(2) 若 $\angle \mathrm{AED}=135^{\circ}$, 探究 $\mathrm{AF}$ 与 $\mathrm{AC}$ 的关系, 并证明;
(3) 如图 2, 延长 $\mathrm{AE}$ 交 $\mathrm{BC}$ 于点 $\mathrm{G}$. 在 (2) 的条件下, 求 $\frac{\mathrm{AE}}{\mathrm{EG}}$ 的值.

如图 1, 在 $\triangle A B C$ 中, $A B=A C, \angle B A C=90^{\circ}$, 点 $D$ 为 $B C$ 中点, $A E \perp B E$, 点 $F$ 为 $A E$ 中点, 连接 $D F$. 点 $G$ 为直线 $E A$ 上一点, 满足 $A G=B E$, 连接 $B G$.
(1) 在图中找出与 $\angle A B E$ 相等的角, 并证明;
(2) 探究 $D F$ 与 $B G$ 的关系, 并证明;
(3) 如图 2, 取 $A B$ 与 $F D$ 交点 $K, B G$ 与 $D F$ 交点 $M$. 若 $A B=\sqrt{5}, B E=1$, 求 $K M$ 的 长.

如图 1, 在 $\triangle A B C$ 中, $\angle B A C=90^{\circ}, A B=A C$, 点 $D$ 为 $B C$ 中点, 点 $E$ 为 $\triangle A B C$ 内一 点, 连接 $B E, E C, \angle B E C=135^{\circ}$, 连接 $A E 、 D E$.
(1) 在图中找出与 $\angle A B E$ 相等的角, 并证明;
(2) 探究线段 $A E$ 与 $D E$ 的数量关系, 并证明;
(3) 如图 2, 若 $C E^2+2 A E^2=B E^2, A E=1$, 求 $A B$ 的值.