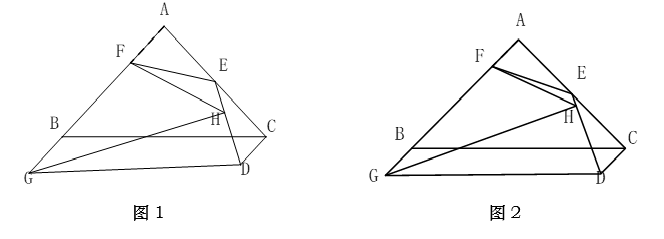
如图 1, 在 $\triangle A B C$ 中, $A B=A C, C D / / A B$, 点 $E$ 为 $A C$ 中点, 连接 $D E$. 以点 $E$ 为圆心, $D E$ 为半径作弧交 $A B$ 于 $F$. 点 $G$ 在 $A B$ 延长线上, 连接 $G D$. 过 $G$ 作 $G H \perp D E$ 于 $H$, 连 接 $\mathrm{HF}$. 若 $\angle \mathrm{FGD}=45^{\circ}$.
(1) 在图中找出与 $\angle \mathrm{AFE}$ 相等的角, 并证明;
(2) 求 $\angle \mathrm{FHG}$ 的度数;
(3) 如图 2, 当 $\mathrm{BG}=\mathrm{CD}=1, \mathrm{AB}=4$, 求 $\mathrm{EH}$ 的长.
(1) 在图中找出与 $\angle \mathrm{AFE}$ 相等的角, 并证明;
(2) 求 $\angle \mathrm{FHG}$ 的度数;
(3) 如图 2, 当 $\mathrm{BG}=\mathrm{CD}=1, \mathrm{AB}=4$, 求 $\mathrm{EH}$ 的长.
