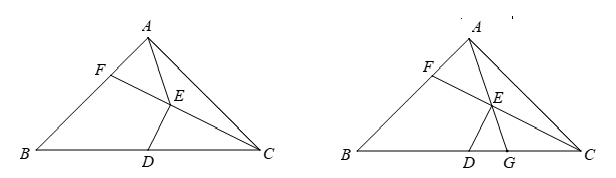
如图 1, 在等腰 Rt $\triangle A B C$ 中, $A B=A C$, 点 $D$ 为 $B C$ 的中点. 点 $F$ 为 $A B$ 边上一点, 连接 $\mathrm{CF}$, 过点 $\mathrm{D}$ 作 $\mathrm{DE} \perp \mathrm{CF}$ 于点 $\mathrm{E}$, 连接 $\mathrm{AE}$.
(1) 探究 $\angle \mathrm{EDC}$ 与 $\angle \mathrm{AFC}$ 间的数量关系, 并证明;
(2) 若 $\angle \mathrm{AED}=135^{\circ}$, 探究 $\mathrm{AF}$ 与 $\mathrm{AC}$ 的关系, 并证明;
(3) 如图 2, 延长 $\mathrm{AE}$ 交 $\mathrm{BC}$ 于点 $\mathrm{G}$. 在 (2) 的条件下, 求 $\frac{\mathrm{AE}}{\mathrm{EG}}$ 的值.
(1) 探究 $\angle \mathrm{EDC}$ 与 $\angle \mathrm{AFC}$ 间的数量关系, 并证明;
(2) 若 $\angle \mathrm{AED}=135^{\circ}$, 探究 $\mathrm{AF}$ 与 $\mathrm{AC}$ 的关系, 并证明;
(3) 如图 2, 延长 $\mathrm{AE}$ 交 $\mathrm{BC}$ 于点 $\mathrm{G}$. 在 (2) 的条件下, 求 $\frac{\mathrm{AE}}{\mathrm{EG}}$ 的值.
