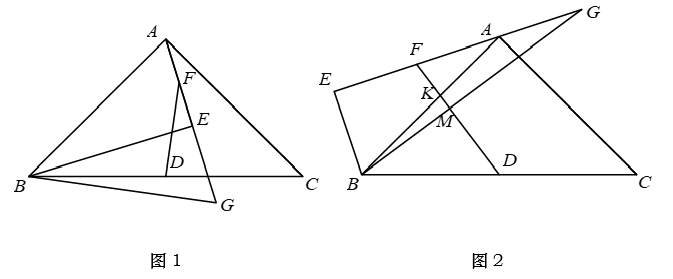
如图 1, 在 $\triangle A B C$ 中, $A B=A C, \angle B A C=90^{\circ}$, 点 $D$ 为 $B C$ 中点, $A E \perp B E$, 点 $F$ 为 $A E$ 中点, 连接 $D F$. 点 $G$ 为直线 $E A$ 上一点, 满足 $A G=B E$, 连接 $B G$.
(1) 在图中找出与 $\angle A B E$ 相等的角, 并证明;
(2) 探究 $D F$ 与 $B G$ 的关系, 并证明;
(3) 如图 2, 取 $A B$ 与 $F D$ 交点 $K, B G$ 与 $D F$ 交点 $M$. 若 $A B=\sqrt{5}, B E=1$, 求 $K M$ 的 长.