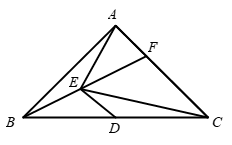
如图, 在 Rt $\triangle A B C$ 中, $A B=A C$, 点 $F$ 为 $A C$ 上一点, 连接 $B F$, 以点 $C$ 为圆心, $C A$ 长 为半径作弧交 $B F$ 于点 $E$, 连接 $A E$. 点 $D$ 为 $B C$ 中点, 连接 $D E$.
(1) 求证: $\angle \mathrm{ACE}=2 \angle \mathrm{BAE}$;
(2) 探究 $\mathrm{BE}$ 与 $\mathrm{DE}$ 的数量关系, 并证明;
(3) 若 $\mathrm{AF}=1, \mathrm{CF}=2$, 求 $\mathrm{EF}$ 的长.
(1) 求证: $\angle \mathrm{ACE}=2 \angle \mathrm{BAE}$;
(2) 探究 $\mathrm{BE}$ 与 $\mathrm{DE}$ 的数量关系, 并证明;
(3) 若 $\mathrm{AF}=1, \mathrm{CF}=2$, 求 $\mathrm{EF}$ 的长.
