单选题 (共 10 题 ),每题只有一个选项正确
-5 的绝对值为
$\text{A.}$ -5
$\text{B.}$ 5
$\text{C.}$ $-\frac{1}{5}$
$\text{D.}$ $\frac{1}{5}$
下列运算正确的是
$\text{A.}$ $(-2)^3=-6$
$\text{B.}$ $x^2 \cdot x^3=x^6$
$\text{C.}$ $\left(x^3\right)^2=x^6$
$\text{D.}$ $4 x^2-2 x=2 x$
下列几何体均由5个大小相同的小立方体搭成, 其中主视图与俯视图相同的是
$\text{A.}$ 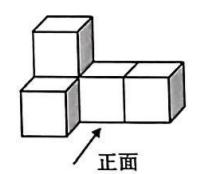 $\text{B.}$
$\text{B.}$ 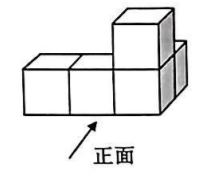 $\text{C.}$
$\text{C.}$ 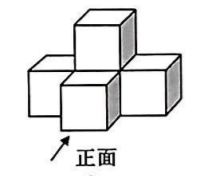 $\text{D.}$
$\text{D.}$ 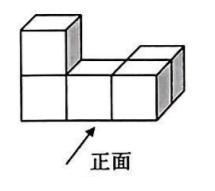
国网山西省电力公司数据显示, 截至 2022 年底, 山西全省新能源装机容量达 4013.52 万千瓦,突破 4000 万千瓦大关,占全省总装机容量的 $33.23 \%$. 数据 4013.52 万千瓦可 用科学记数法表示为

$\text{A.}$ $401352 \times 10^2$ 千瓦
$\text{B.}$ $4013.52 \times 10^4$ 千瓦
$\text{C.}$ $4.01352 \times 10^7$ 千瓦
$\text{D.}$ $4.01352 \times 10^8$ 千瓦
如图, 直线 $a / / b, \angle 1=55^{\circ}, \angle 2=90^{\circ}$, 则 $\angle 3$ 的度数为
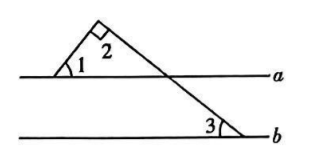
$\text{A.}$ $35^{\circ}$
$\text{B.}$ $40^{\circ}$
$\text{C.}$ $45^{\circ}$
$\text{D.}$ $55^{\circ}$
三国时期的数学家赵爽在其所著的《勾股圆方图注》中记载了一元二次方程的几何解 法, 例如可构造如图所示的图形求解方程 $x(x+2)=15$, 这一过程体现的数学思想是
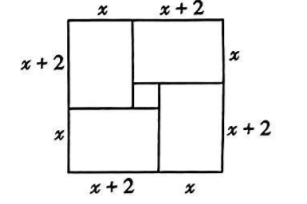
$\text{A.}$ 统计思想
$\text{B.}$ 化归思想
$\text{C.}$ 分类讨论思想
$\text{D.}$ 数形结合思想
如图, 反比例函数 $y_1=\frac{k}{x}(k \neq 0)$ 的图象与正比例函数 $y_2=m x(m \neq 0)$ 的图象相交于 $A$, $B$ 两点, 点 $A$ 的横坐标为 -1 . 当 $y_1>y_2>0$ 时, $x$ 的取值范围是
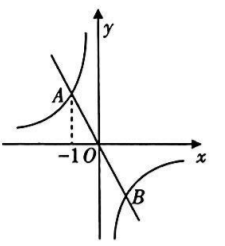
$\text{A.}$ $-1 < x < 0$
$\text{B.}$ $x < -1$
$\text{C.}$ $x>1$
$\text{D.}$ $-1 < x < 0$ 或 $x>1$
如图, 四边形 $A B C D$ 内接于 $\odot O$, 连接 $O A, O C$. 若 $A D / / B C, \angle B A D=70^{\circ}$, 则 $\angle A O C$ 的度数为
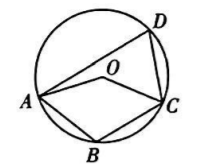
$\text{A.}$ $110^{\circ}$
$\text{B.}$ $120^{\circ}$
$\text{C.}$ $130^{\circ}$
$\text{D.}$ $140^{\circ}$
九年(1)班甲、乙、丙、丁四位同学最近 6 次信息技术模拟测试成绩(单位: 分, 满分 10 分)的平均数和方差如下表所示:

根据表中数据, 成绩好且发挥稳定的同学是
$\text{A.}$ 甲
$\text{B.}$ 乙
$\text{C.}$ 丙
$\text{D.}$ 丁
如图, 在 Rt $\triangle A B C$ 中, $\angle C=90^{\circ}, \angle A=30^{\circ}, A B=6$, 以点 $C$ 为圆心, $C B$ 的长为半径画弧, 交 $A B$ 于点 $D$, 交 $A C$ 于点 $E$, 则图中阴影部分的面积为
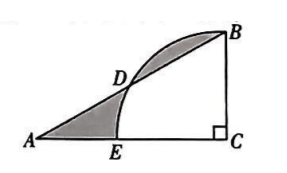
$\text{A.}$ $\frac{3}{2} \pi-\frac{9}{4} \sqrt{3}$
$\text{B.}$ $\frac{3}{4} \pi-\frac{9}{8} \sqrt{3}$
$\text{C.}$ $\frac{3}{4} \pi$
$\text{D.}$ $\frac{3}{2} \pi$
填空题 (共 5 题 ),请把答案直接填写在答题纸上
计算 $(\sqrt{8}+2)(\sqrt{8}-2)$ 的结果为
在一个不透明的袋子中装有三个编号分别为 $1,2,3$ 的小球, 三个小球除编号外完全相 同, 小明将袋子中的小球摇匀后从中随机摸出一个并记下编号, 然后放回袋中摇匀, 再从袋子中随机摸出一个小球并记下编号, 则两次所摸小球的编号之积为奇数的概率为
如图, 在 $\triangle A B C$ 中, $\angle B A C=36^{\circ}$, 将 $\triangle A B C$ 绕点 $A$ 顺时针旋转得到 $\triangle A B^{\prime} C^{\prime}$, 连接 $C C^{\prime}$, 当点 $B$ 的对应点 $B^{\prime}$ 落在 $A C$ 边上时, $\angle B^{\prime} C C^{\prime}$ 的度数为

春节期间电影《满江红》的公映带火拍摄地太原古县城, 太原古县城也因此迎来了旅 游的高峰期. 据了解, 今年 1 月份第一周该景点参观人数约 10 万人,第三周参观人数增 加到约 25.6 万人, 这两周参观人数的平均增长率为
如图, 已知四边形 $A B C D$ 是边长为 4 的正方形, 点 $E$ 是 $B C$ 边的中点, 连接 $D E$, 将 $\triangle D C E$ 沿 $D E$ 翻折得到 $\triangle D C^{\prime} E$, 连接 $A C^{\prime}$, 则 $A C^{\prime}$ 的长为
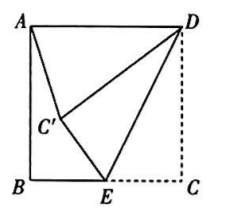
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
(1)计算: $(-2)^2+15 \div(-3)+\left(\frac{1}{2}\right)^{-1}$.
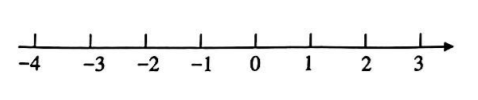
(2) 解不等式组: $\left\{\begin{array}{l}2 x+5 \geqslant 3(x+1), \\ \frac{x+1}{2}>\frac{x}{3},\end{array}\right.$ 并将其解集表示在如图所示的数轴上.
如图, 已知 $A B / / C D$, 且 $A B=C D$, 连接 $B D$, 作 $A E \perp B D$ 于点 $E, C F \perp B D$ 于点 $F$, 连接 $A F, C E$. 猜想四边形 $A E C F$ 的形状, 并说明理由.

闻喜花馍享誉全国, 是闻喜人民用当地生产的优质小麦粉, 经和面后, 采用捏, 㦈, 揉, 拽, 剪, 贴等多道工艺, 捏出花 果、人物、鸟兽等栩栩如生的形象, 再经过蒸制、晾晒、着色制作 而成. 某展览会上展销闻喜花馍, 王阿姨购买了 2 个 A 型花馍和 3 个 $B$ 型花馍共花费 480 元, 李阿姨购买了 3 个 $A$ 型花馍和 2 个 $B$ 型花馍共花费 520 元, 分别求出 $A$ 型、 $B$ 型花馍的单价.

综合与实践是一类以问题为载体, 以学生自主参与为主的学习活动, 它搭 建了课程学习和实践应用之间的桥梁. 学校为了解综合与实践活动的开展情况, 组织 全体学生进行了一次关于“每周参与综合与实践活动情况” 的问卷调查, 并准备随机 抽取 200 名学生的问卷进行统计分析.
【数据收集】
(1)学校设计了以下四种抽样调查方案:
方案 1 : 在九年级学生中随机抽取 200 名学生的问卷;
方案 2 : 在七年级学生中随机抽取 200 名学生的问卷;
方案 3 : 在全校男生中随机抽取 200 名学生的问卷;
方案 4 : 在全校学生中随机抽取 200 名学生的问卷.
其中最合理的方案是 ________
【数据整理】
学校按最合理的方案进行抽样, 经过对问卷数据的整理,得到如下结果.
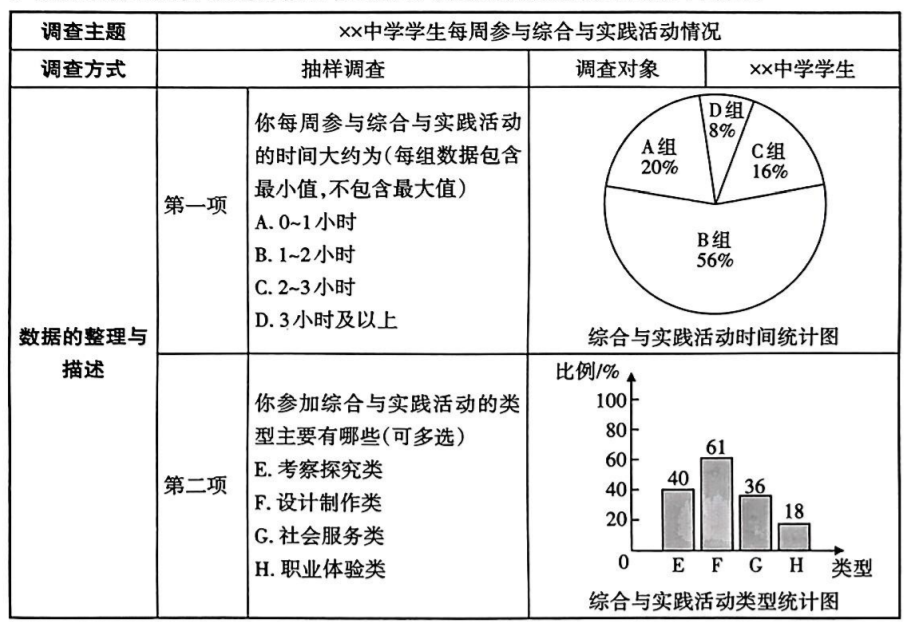
【数据分析】
(2) 若该校共有 1800 名学生, 请估计每周参与综合与实践活动不低于 2 小时的学生人 数与选择 “考察探究类”的人数.
(3) 九年(1)班要根据以上调查结果对全校学生综合与实践活动情况进行分析, 假如 你是该班的学生, 请你结合以上两项调查报告数据分别写出一条通过分析获取的 信息.
阅读与思考
下面是小宇同学课外阅读的一则数学材料, 请仔细阅读并完成相应任务.
“真分式”与“假分式”
我们知道, 假分数可以化为整数与真分数的和的形式, 例如: $\frac{3}{2}=1+\frac{1}{2}$. 在分式中, 对于 只含有一个字母的分式, 当分子的次数大于或等于分母的次数时,我们称之为假分式;当分子 的次数小于分母的次数时, 我们称之为真分式, 如 $\frac{x+1}{x-1}, \frac{x^2}{x-2} \cdots$ 这样的分式是假分式; 如 $\frac{x-1}{x^2+1}, \frac{5}{x^2+2} \cdots$ 这样的分式是真分式. 类似地, 假分式也可以化为整式与真分式的和的 形式.
例如:
将分式 $\frac{x-2}{x+3}$ 化成一个整式与一个真分式的和的形式,过程如下:
$$
\frac{x-2}{x+3}=\frac{(x+3)-3-2}{x+3}=\frac{(x+3)-5}{x+3}=1-\frac{5}{x+3} \text {. }
$$
将分式 $\frac{x^2+4 x-5}{x+3}$ 化成一个整式与一个真分式的和的形式, 过程如下:
方法 $1: \frac{x^2+4 x-5}{x+3}=\frac{x^2+3 x+x-5}{x+3}=\frac{x(x+3)+(x+3)-8}{x+3}=x+1-\frac{8}{x+3}$.
方法 2: 由于分母为 $x+3$, 可设 $x^2+4 x-5=(x+3)(x+a)+b(a, b$ 为常数 $)$,
$$
\begin{aligned}
& \because(x+3)(x+a)+b=x^2+a x+3 x+3 a+b=x^2+(a+3) x+(3 a+b), \\
& \therefore x^2+4 x-5=x^2+(a+3) x+(3 a+b) . \\
& \therefore\left\{\begin{array} { l }
{ a + 3 = 4 , } \\
{ 3 a + b = - 5 . }
\end{array} \text { 解得 } \left\{\begin{array}{l}
a=1, \\
b=-8 .
\end{array}\right.\right. \\
& \therefore x^2+4 x-5=(x+3)(x+1)-8 . \\
& \therefore \frac{x^2+4 x-5}{x+3}=\frac{(x+3)(x+1)-8}{x+3}=\frac{(x+3)(x+1)}{x+3}-\frac{8}{x+3}=x+1-\frac{8}{x+3} .
\end{aligned}
$$
这样, 分式 $\frac{x^2+4 x-5}{x+3}$ 就被化成了一个整式与一个真分式的和的形式.
任务:
(1) 分式 $\frac{2}{x+3}$ 是 ________ 分式 (填 “真”或 “假” ); 将假分式 $\frac{2 x+3}{x}$ 化为一个整式与一个 真分式的和的形式为 ________
(2)请将 $\frac{x^2+2 x-14}{x-3}$ 化为一个整式与一个真分式的和的形式.
(3)若分式 $\frac{x^2+2 x-14}{x-3}$ 的值为整数, 请根据(2)的结果直接写出符合条件的 2 个 $x$ 的值.
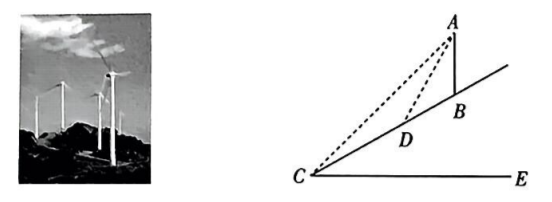
“风电”是末来全球最重要的清洁能源之一. 在我们的身边也经常能见到 “风电”的身影,这些祭立在高山、草原上的“大风车”构成了一道道亮丽的风景线. 周 日, 某校项目学习小组的同学来到郊外山脚下, 计划测量一座风力发电机组的塔筒 $A B$ 的高度. 如图, 斜坡 $C B$ 的坡角 $\angle B C E=30^{\circ}$, 小颖同学在坡底 $C$ 处测得塔筒顶端 $A$ 的仰 角为 $45^{\circ}$, 小颖沿坡面 $C B$ 前行 $120 \mathrm{~m}$ 到达 $D$ 处, 测得塔筒顶端 $A$ 的仰角为 $60^{\circ}$. 其中点 $A, B, C, D, E$ 均在同一竖直平面内. 请根据以上数据求塔筒 $A B$ 的高度. (结果精确到 $1 \mathrm{~m}$. 参考数据: $\sqrt{2} \approx 1.41, \sqrt{3} \approx 1.73$ )
综合与实践
问题情境
四边形 $A B C D$ 是边长为 5 的菱形, 连接 $B D$. 将 $\triangle B C D$ 绕点 $B$ 按顺时针方向旋转得到 $\triangle B E F$, 点 $C, D$ 旋转后的对应点分别为 $E, F$. 旋转角为 $\alpha\left(0^{\circ} < \alpha < 360^{\circ}\right)$.
观察思考
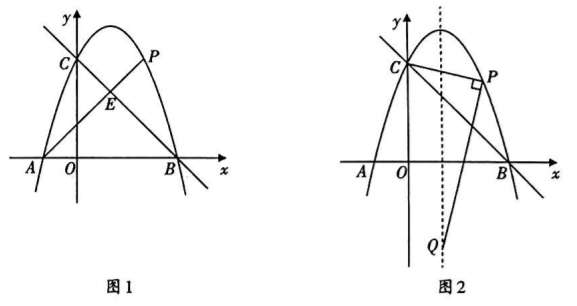
(1) 如图 1, 连接 $A C$, 当点 $F$ 第一次落在对角线 $A C$ 上时, $\alpha=$ 探究证明
(2)如图 2, 当 $\alpha>180^{\circ}$, 且 $E F / / B D$ 时, $E F$ 与 $A D$ 交于点 $G$. 试判断四边形 $B D G F$ 的形状, 并说明理由.
拓展延伸
(3) 如图 3, 连接 $C E$. 在旋转过程中, 当 $E F$ 与菱形 $A B C D$ 的一边平行时, 且 $\tan \angle D A B=$ $\frac{3}{4}$, 请直接写出线段 $C E$ 的长.

综合与探究
如图 1, 已知抛物线 $y=-x^2+b x+c$ 与 $x$ 轴交于 $A, B$ 两点, 与 $y$ 轴交于点 $C$, 且 $A(-1,0)$, $C(0,3)$. 点 $P$ 是抛物线上的一个动点.
(1) 求抛物线的函数表达式,并直接写出直线 $B C$ 的函数表达式.
(2) 如图 1, 当点 $P$ 在直线 $B C$ 上方时, 连接 $A P$ 交 $B C$ 于点 $E$, 当 $P E=\frac{1}{2} A E$ 时, 求点 $P$ 的 坐标.
(3) 如图 2, 连接 $C P$, 过点 $P$ 作 $Q P \perp C P$ 交抛物线的对称轴于点 $Q$. 试探究 : 是否存在 一点 $P$ 使 $C P=Q P$. 若存在, 请直接写出点 $P$ 的坐标; 若不存在, 请说明理由.