综合与探究
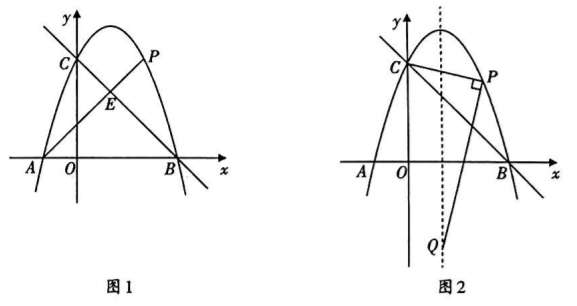
如图 1, 已知抛物线 $y=-x^2+b x+c$ 与 $x$ 轴交于 $A, B$ 两点, 与 $y$ 轴交于点 $C$, 且 $A(-1,0)$, $C(0,3)$. 点 $P$ 是抛物线上的一个动点.
(1) 求抛物线的函数表达式,并直接写出直线 $B C$ 的函数表达式.
(2) 如图 1, 当点 $P$ 在直线 $B C$ 上方时, 连接 $A P$ 交 $B C$ 于点 $E$, 当 $P E=\frac{1}{2} A E$ 时, 求点 $P$ 的 坐标.
(3) 如图 2, 连接 $C P$, 过点 $P$ 作 $Q P \perp C P$ 交抛物线的对称轴于点 $Q$. 试探究 : 是否存在 一点 $P$ 使 $C P=Q P$. 若存在, 请直接写出点 $P$ 的坐标; 若不存在, 请说明理由.