单选题 (共 11 题 ),每题只有一个选项正确
点 $(0,-1)$ 到直线 $y=k(x+1)$ 距离的最大值为 ()
$\text{A.}$ 1
$\text{B.}$ $\sqrt{2}$
$\text{C.}$ $\sqrt{3}$
$\text{D.}$ 2
已知 $a \in \mathbf{R}$ ,则直线 $l_{1}: x+a y-1=0$ 与直线 $l_{2}:(1-a) x+2 a y-1=0$ 平行的充要条件是
$\text{A.}$ $a \neq 0$
$\text{B.}$ $a=0$
$\text{C.}$ $a=-1$
$\text{D.}$ $a=0$ 或 $a=-1$
已知直线 $l_{1}: x-3 y=0, l_{2}: x+a y-2=0$ ,若 $l_{1} \perp l_{2}$ ,则 $a$ 的值为 $($
$\text{A.}$ $\frac{1}{3}$
$\text{B.}$ $-\frac{1}{3}$
$\text{C.}$ 3
$\text{D.}$ -3
"$a=3$"是"直线 $a x+y-3=0$ 与 $3 x+(a-2) y+4=0$ 平行"的
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分又不必要条件
"$m=-1$"是"直线 $x+m y-2=0$ 与直线 $x-y+n=0$ 平行"的( )
$\text{A.}$ 充分不必要条件
$\text{B.}$ 必要不充分条件
$\text{C.}$ 充要条件
$\text{D.}$ 既不充分也不必要条件
三条直线 $l_{1}: x-y=0, l_{2}: x+y-2=0, l_{3}: 5 x-k y-15=0$ 构成一个三角形,则 $k$ 的取值范围是( )
$\text{A.}$ $k \in \mathbf{R}$
$\text{B.}$ $k \in \mathbf{R}$ 且 $k \neq \pm 1, k \neq 0$
$\text{C.}$ $k \in \mathbf{R}$ 且 $k \neq \pm 5, k \neq-10$
$\text{D.}$ $k \in \boldsymbol{R}$ 且 $k \neq \pm 5, k \neq 1$
若直线 $l_{1}: x+m y+1=0$ 与 $l: 2 x-y=0$ 垂直,直线 $l_{2}$ 的方程为 $2 x+2 m y+3=0$ ,则 $l_{1}$与 $l_{2}$ 间的距离为
$\text{A.}$ $\frac{2 \sqrt{5}}{5}$
$\text{B.}$ $\frac{4 \sqrt{5}}{5}$
$\text{C.}$ $\frac{\sqrt{5}}{10}$
$\text{D.}$ $\frac{\sqrt{5}}{5}$
已知两点 $A(1,2), B(3,6)$ ,动点 $M$ 在直线 $y=x$ 上运动,则 $|M A|+|M B|$ 的最小值为
$\text{A.}$ $2 \sqrt{5}$
$\text{B.}$ $\sqrt{26}$
$\text{C.}$ 4
$\text{D.}$ 5
已知 $m \in \mathbf{R}$ ,过定点 $A$ 的动直线 $m x+y=0$ 和过定点 $B$ 的动直线 $x-m y-m+3=0$ 交于点 $P$ ,则 $|P A|+\sqrt{3}|P B|$ 的取值范围是( )
$\text{A.}$ $(\sqrt{10}, 2 \sqrt{10}]$
$\text{B.}$ $(\sqrt{10}, \sqrt{30}]$
$\text{C.}$ $[\sqrt{10}, \sqrt{30})$
$\text{D.}$ $[\sqrt{10}, 2 \sqrt{10}]$
已知直线 $l_1: a x-y+1=0, l_2: x+a y+1=0, a \in \mathbf{R}$ ,以下结论不正确的是( )
$\text{A.}$ 不论 $a$ 为何值时,$l_1$ 与 $l_2$ 都互相垂直
$\text{B.}$ 当 $a$ 变化时,$l_1$ 与 $l_2$ 分别经过定点 $A(0,1)$ 和 $B(-1,0)$
$\text{C.}$ 不论 $a$ 为何值,$l_1$ 与 $l_2$ 都关于直线 $x+y=0$ 对称
$\text{D.}$ 如果 $l_1$ 与 $l_2$ 交于点 $M, O$ 为坐标原点,则 $|M O|$ 的最大值是 $\sqrt{2}$
定义点 $P\left(x_0, y_0\right)$ 到直线 $l: a x+b y+c=0\left(a^2+b^2 \neq 0\right)$ 的有向距离为 $d=\frac{a x_0+b y_0+c}{\sqrt{a^2+b^2}}$ .已知点 $P_1, P_2$ 到直线 $l$ 的有向距离分别是 $d_1, d_2$ .以下命题正确的是()
$\text{A.}$ 若 $d_1=d_2=1$ ,则直线 $P_1 P_2$ 与直线 $l$ 平行
$\text{B.}$ 若 $d_1=1, d_2=-1$ ,则直线 $P_1 P_2$ 与直线 $l$ 垂直
$\text{C.}$ 若 $d_1+d_2=0$ ,则直线 $P_1 P_2$ 与直线 $l$ 垂直
$\text{D.}$ 若 $d_1 \cdot d_2 \leqslant 0$ ,则直线 $P_1 P_2$ 与直线 $l$ 相交
填空题 (共 2 题 ),请把答案直接填写在答题纸上
已知点 $(a, 2)(a > 0)$ 到直线 $l: x-y+3=0$ 的距离为 1 ,则 $a$ 的值为 $\qquad$ .
若直线 $2 x-y=-10, y=x+1, y=a x-2$ 交于一点,则 $a$ 的值为 $\qquad$ .
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
求经过直线 $l_{1}: 3 x+2 y-1=0$ 和 $l_{2}: 5 x+2 y+1=0$ 的交点,且垂直于直线 $l_{3}: 3 x-5 y+6=$ 0 的直线 $l$ 的方程.
已知点 $\mathrm{P}(2,-1)$ .
(1)求过点 P 且与原点距离为 2 的直线 1 的方程.
(2)求过点 P 且与原点距离最大的直线 1 的方程,并求出最大距离.
(3)是否存在过点 P 且与原点距离为 6 的直线?若存在,求出方程;若不存在,请说明理由。
已知直线 $l: x+2 y-2=0$ .
(1)求直线 $l$ 关于点 $A(1,1)$ 对称的直线方程;
(2)求直线 $l_{1}: y=x-2$ 关于直线 $l$ 对称的直线 $l_{2}$ 的方程.
已知 $\triangle A B C$ 的两个顶点 $A(-1,5)$ 和 $B(0,-1)$ ,若 $\angle A C B$ 的平分线所在的直线方程为 $2 x-3 y+6=0$ ,则 $B C$ 边所在的直线方程为 $\qquad$ ;
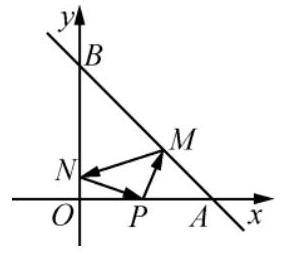
如图,已知点 $A(4,0), B(0,4)$ ,从点 $P(2,0)$ 射出的光线经直线 $A B$ 反射后射到直线 $O B$上,再经直线 $O B$ 反射后又回到点 $P$ ,则光线所经过的路程是 $\qquad$。