单选题 (共 7 题 ),每题只有一个选项正确
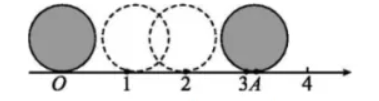
为了证明数轴上的点可以表示无理数,老师给学生设计了如下材料:如图,直径为 1 个单位长度的圆从原点沿数轴向右滚动一周,圆上一点由原点(记为点 $O$ )到达点 $A$ ,点 $A$ 对应的数是多少?从图中可以看出 $O A$的长是这个圆的周长 $\pi$ ,所以点 $A$ 对应的数是 $\pi$ ,这样,无理数 $\pi$ 可以用数轴上的点表示出来,上述材料体现的数学思想是
$\text{A.}$ 方程思想
$\text{B.}$ 从特殊到一般
$\text{C.}$ 数形结合思想
$\text{D.}$ 分类思想
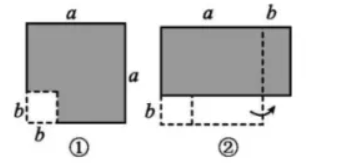
在边长为 $a$ 的正方形中挖去一个边长为 $b$ 的小正方形( $a>b$ )(如图 F2-2(1)),把余下的部分拼成一个长方形 (如图(2)),根据两个图形中阴影部分的面积相等,可以验证
$\text{A.}$ $(a+b)^2=a^2+2 a b+b^2$
$\text{B.}$ $(a-b)^2=a^2-2 a b+b^2$
$\text{C.}$ $(a+2 b)(a-b)=a^2+a b-2 b^2$
$\text{D.}$ $a^2-b^2=(a+b)(a-b)$
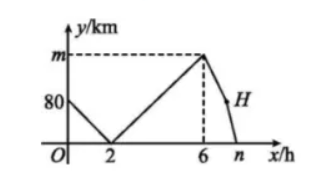
甲、乙两车从 $A$ 地出发,匀速驶向 $B$ 地.甲车以 80 $km / h$ 的速度行驶 1 h 后,乙车才沿相同路线行驶.乙车先到达 $B$ 地并停留 1 h 后,再以原速按原路返回,直至与甲车相遇。在此过程中,两车之间的距离 $y(km)$ 与乙车行驶时间 $x(h)$ 之间的函数关系如图所示。下列说法:(1)乙车的速度是 $120 km / h$ ;(2)$m=160$ ;(3)点 $H$ 的坐标是 $(7,80)$ ;(4)$n=7.5$ .其 中说法正确的有
$\text{A.}$ 4 个
$\text{B.}$ 3 个
$\text{C.}$ 2 个
$\text{D.}$ 1 个
已知二次函数 $y=(x-h)^2+1$( $h$ 为常数),在自变量 $x$ 的值满足 $1 \leq x \leq 3$ 的情况下,与其对应的函数值 $y$ 的最小值为 5 ,则 $h$ 的值为
$\text{A.}$ 1 或- 5
$\text{B.}$ -1 或 5
$\text{C.}$ 1 或-3
$\text{D.}$ 1 或 3
方程 $x^2+2 x-1=0$ 的根可看成函数 $y=x+2$ 的图象与函数 $y=\frac{1}{x}$ 的图象交点的横坐标,用此方法可推断方程 $x^3+x-1=0$ 的实数根有( )
$\text{A.}$ 0 个
$\text{B.}$ 1 个
$\text{C.}$ 2 个
$\text{D.}$ 3 个
已知二次函数 $y=a x^2+b x+c$ 的 $y$ 与 $x$ 的部分对应值如表:
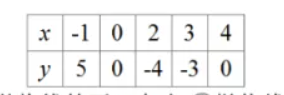
下列结论:(1)抛物线的开口向上;(2)抛物线的对称轴为直线 $x=2$ ;(3)当 $0 < x < 4$ 时,$y>0$ ;(4)抛物线与 $x$ 轴的两个交点间的距离是 $4 ;$(5)若 $A\left(x_1, 2\right), B\left(x_2, 3\right)$ 是抛物线上两点,则 $x_1 < x_2$ .其中正确的个数是()
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
已知 $m>0$ ,关于 $x$ 的一元二次方程 $(x+1)(x-2)-m=0$ 的解为 $x_1, x_2\left(x_1 < x_2\right)$ ,则下列结论正确的是( )
$\text{A.}$ $x_1 < -1 < 2 < x_2$
$\text{B.}$ $-1 < x_1 < 2 < x_2$
$\text{C.}$ $-1 < x_1 < x_2 < 2$
$\text{D.}$ $x_1 < -1 < x_2 < 2$
填空题 (共 10 题 ),请把答案直接填写在答题纸上
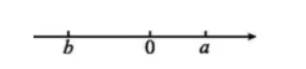
已知实数 $a, b$ 在数轴上的位置如图 F2-4 所示,化简:$\sqrt{(a-b)^2}-|a+b|$ 的结果为
已知关于 $x$ 的不等式组 $\left\{\begin{array}{l}x-a>0, \\ 3-x>0\end{array}\right.$ 的整数解共有 2 个,则 $a$ 的取值范围为
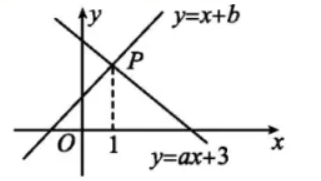
如图 F2-5,已知函数 $y=x+b$ 和 $y=a x+3$ 的图象交点为 $P$ ,则不等式 $x+b>a x+3$ 的解集为
《庄子.天下篇》中写道:"一尺之棰,日取其半,万世不竭."意思是:一根一尺的木棍,如果每天截取它的一半,永远也取不完,如图 F2-6.
由图易得:$\frac{1}{2}+\frac{1}{2^2}+\frac{1}{2^3}+\ldots+\frac{1}{2^n}=$ $\qquad$ .
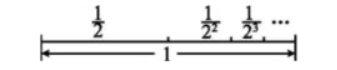
当 $x=m$ 和 $x=n(m \neq n)$ 时,代数式 $x^2-2 x+3$ 的值相等,则 $x=m+n$ 时,代数式 $x^2-2 x+3$ 的值为 $\qquad$。
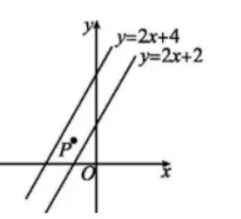
如图,在平面直角坐标系中,点 $P(-1, a)$ 在直线 $y=2 x+2$ 与直线 $y=2 x+4$ 之间,则 $a$ 的取值范围是 $\qquad$ .
已知函数 $y=\left\{\begin{array}{l}(x-1)^2+1(x < 2), \\ (x-4)^2-2(x \geq 2),\end{array}\right.$ 使 $y=k$ 成立的 $x$ 的值恰好只有 3 个时,$k$ 的值为
已知 $\odot O$ 的直径 $A B=2$ ,过点 $A$ 有两条弦,$A C=\sqrt{2}, A D=\sqrt{3}$ ,则 $\angle C A D$ 的度数为
如图,矩形纸片 $A B C D$ 的长 $A D=9 cm$ ,宽 $A B=3 cm$ ,将其折叠,使点 $D$ 与点 $B$ 重合,则折叠后 $D E$ 的长为 $\qquad$ cm ,折痕 $E F$ 的长为 $\qquad$ cm .
在平面直角坐标系中,$\odot A$ 的半径为 2 ,点 $A$ 的坐标为 $(5,12), P(m, n)$ 是 $\odot A$ 上的一个动点,则 $m^2+n^2$ 的最大值为
解答题 (共 2 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
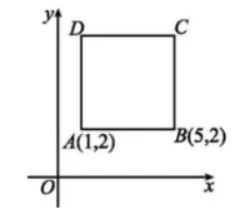
如图 F2-9,四边形 $A B C D$ 是一个正方形,已知 $A(1,2), B(5,2)$ .
(1)求点 $C, D$ 的坐标;
(2)若一次函数 $y=k x-2$ 的图象过 $C$ 点,求 $k$ 的值;
(3)若直线 $y=k x-2$ 与正方形 $A B C D$ 有交点,求 $k$ 的取值范围.
已知函数 $y=x^2+b x+c$( $b, c$ 为常数)的图象经过点 $(-2,4)$ .
(1)求 $b, c$ 满足的关系式;
(2)设该函数图象的顶点坐标是 $(m, n)$ ,当 $b$ 的值变化时,求 $n$ 关于 $m$ 的函数解析式;
(3)若该函数的图象不经过第三象限,当 $-5 \leq x \leq 1$ 时,函数的最大值与最小值之差为 16 ,求 $b$ 的值.