单选题 (共 3 题 ),每题只有一个选项正确
设两个相互独立的随机变量 $X$ 和 $Y$ 的方差分别为 4 和 2 ,则随机变量 $3 X-2 Y$ 的方差是( )。
$\text{A.}$ 8
$\text{B.}$ 16
$\text{C.}$ 28
$\text{D.}$ 44
已知随机变量 $X$ 服从二项分布,且 $E X=2.4, D X=1.44$ ,则二项分布的参数 $n, p$的值为( )。
$\text{A.}$ $n=4, p=0.6$
$\text{B.}$ $n=6, p=0.4$
$\text{C.}$ $n=8, p=0.3$
$\text{D.}$ $n=24, p=0.1$
将一枚硬市重复掷 $n$ 次,以 $X$ 和 $Y$ 分别表示正面向上和反面向上的次数,则 $X$ 和 $Y$的相关系数等于 $\qquad$。
$\text{A.}$ -1
$\text{B.}$ 0
$\text{C.}$ $\frac{1}{2}$
$\text{D.}$ 1
填空题 (共 4 题 ),请把答案直接填写在答题纸上
设离散型随机变量 $X$ 的分布律为:$P\left\{X=2^k\right\}=\frac{2}{3^k}, k=1,2, \cdots$ ,则 $E(X)=$
设随机变量 $X$ 的分布律为 $P\left\{X=(-1)^k k\right\}=\frac{1}{k(k+1)}(k=1,2, \cdots)$ .求 $X$ 的数学期望.
设在某一规定的时间间隔里,某电气设备用于最大负荷的时间 $X$(以分计)是一个随机变量,其概率密度为
$$
f(x)= \begin{cases}\frac{1}{(1500)^2} x, & 0 \leqslant x \leqslant 1500 \\ \frac{-1}{(1500)^2}(x-3000), & 1500 < x \leqslant 3000 \\ 0, & \text { 其他 }\end{cases}
$$
求 $E(X)$ .
设随机变量 $X$ 的分布函数为
$$
F(x)= \begin{cases}1-\frac{4}{x^2}, & x \geqslant 2 \\ 0, & x < 2\end{cases}
$$
求 $X$ 的期望.
解答题 (共 13 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
从甲地到乙地的旅游车上载 20 位旅客自甲地开出,沿途有 10 个车站,如到达一个车站没有旅客下车就不停车.以 $X$ 表示停车次数,求 $E(X)$(设每位旅客在各个车站下车是等可能的)。
游客乘电梯从底层到电视塔顶层观光.电梯于每个整点的第 5 分钟、 25 分钟和 55分钟从底层起行,假设一游客在早八点的第 $X$ 分钟到达底层候梯处,且 $X$ 在 $[0,60]$ 上均匀分布,求该游客等候时间的数学期望.
设随机变量 $X$ 服从几何分布,其分布律为
$$
P\{X=k\}=p(1-p)^{k-1}, \quad k=1,2, \cdots
$$
其中 $0 < p < 1$ 是常数,求 $E(X), D(X)$ .
设随机变量 $(X, Y)$ 具有概率密度函数
$$
f(x, y)= \begin{cases}\frac{1}{8}(x+y), & 0 \leqslant x \leqslant 2,0 \leqslant y \leqslant 2 \\ 0, & \text { 其他 }\end{cases}
$$
求 $E(X), E(Y), \operatorname{Cov}(X, Y), \rho_{X Y}, D(X+Y)$ .
设二维随机变量 $(X, Y)$ 的联合概率密度为
$$
f(x, y)= \begin{cases}y e^{-(x+y)}, & x, y>0 \\ 0, & \text { 其他 }\end{cases}
$$
试求 $X, Y$ 是否相关,是否独立.
设随机变量 $(X, Y)$ 的分布律为
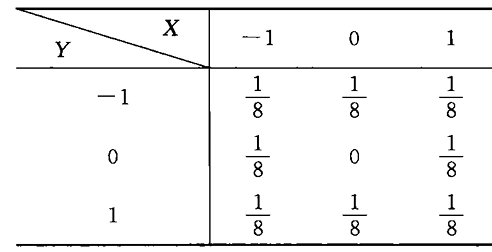
验证 $X$ 和 $Y$ 是不相关的,但 $X$ 和 $Y$ 不是相互独立的.
设随机变量 $X$ 在 $[a, b]$ 上服从均匀分布,求 $X$ 的 $k$ 阶原点矩和三阶中心矩.
假设随机变量 $U$ 在区间 $[-2,2]$ 上服从均匀分布,随机变量
$$
X=\left\{\begin{array}{rl}
-1, & \text { 若 } U \leqslant-1 \\
1, & \text { 若 } U>-1
\end{array} \quad Y=\left\{\begin{aligned}
-1, & \text { 若 } U \leqslant 1 \\
1, & \text { 若 } U>1
\end{aligned}\right.\right.
$$
试求:(1)$X$ 和 $Y$ 的联合概率分布;
$D(X+Y)$ .
对于任意二事件 $A$ 和 $B, 0 < P(A) < 1,0 < P(B) < 1$ ,
$$
\rho=\frac{P(A B)-P(A) P(B)}{\sqrt{P(A) P(B) P(\bar{A}) P(\bar{B})}}
$$
称做事件 $A$ 和 $B$ 的相关系数.
(1)证明事件 $A$ 和 $B$ 独立的充分必要条件是其相关系数等于零;
(2)利用随机变量相关系数的基本性质,证明 $|\rho| \leqslant 1$ .
若 $X \sim N(0,1)$ ,且 $Y=X^2$ ,问 $X$ 与 $Y$ 是否不相关?是否相互独立?
一商店经销某种商品,每周进货的数量 $X$ 与顾客对该种商品的需求量 $Y$ 是相互独立的随机变量,且都服从区间 $[10,20]$ 上的均匀分布.商店每售出一单位商品可得利润 1000 元;若需求量超过了进货量,商店可从其他商店调剂供应,这时每单位商品获利润 500 元。试计算此商店经销该种商品每周所得利润的期望值.
从学校乘汽车到火车站的途中有 3 个交通岗,假设在各个交通岗遇到红灯的事件是相互独立的,并且概率都是 $\frac{2}{5}$ ,设 $X$ 为途中遇到红灯的次数,求随机变量 $X$ 的分布律、分布函数和数学期望.
设二维随机变量 $(X, Y)$ 的密度函数为
$$
f(x, y)=\frac{1}{2}\left[\varphi_1(x, y)+\varphi_2(x, y)\right]
$$
其中 $\varphi_1(x, y)$ 和 $\varphi_2(x, y)$ 都是二维正态密度函数,且它们对应的二维随机变量的相关系数分别为 $\frac{1}{3}$ 和 $-\frac{1}{3}$ ,它们的边缘密度函数所对应的随机变量的数学期望都是零,方差都是 1 。
(1)求随机变量 $X$ 和 $Y$ 的密度函数 $f_1(x)$ 和 $f_2(y)$ ,及 $X$ 和 $Y$ 的相关系数 $\rho$(可以直接利用二维正态密度的性质).
(2)问 $X$ 和 $Y$ 是否独立?为什么?