单选题 (共 10 题 ),每题只有一个选项正确
计算 $-2-8$的结果是
$\text{A.}$ $-6$
$\text{B.}$ $-10$
$\text{C.}$ $10$
$\text{D.}$ $6$
据科学家估计,地球的年龄大约是 4600000000 年,将数据 4600000000 用科学记数法表示应为
$\text{A.}$ $0.46 \times 10^{10}$
$\text{B.}$ $4.6 \times 10^9$
$\text{C.}$ $46 \times 10^8$
$\text{D.}$ $4.6 \times 10^8$
高速公路是指专供汽车高速行驶的公路.高速公路在建设过程中,通常要从大山中开挖隧道穿过,把道路取直以缩短路程. 其中的数学原理是

$\text{A.}$ 两点之间线段最短
$\text{B.}$ 两点确定一条直线
$\text{C.}$ 平行线之间的距离最短
$\text{D.}$ 平面内经过一点有无数条直线
下列函数中,函数值 $y$ 随 $x$ 的增大而减小的是
$\text{A.}$ $y=6 x$
$\text{B.}$ $y=-6 x$
$\text{C.}$ $y=\frac{6}{x}$
$\text{D.}$ $y=-\frac{6}{x}$
若 $a>b$ ,则下列不等关系一定成立的是
$\text{A.}$ $a+c>b+c$
$\text{B.}$ $a-c < b-c$
$\text{C.}$ $a c>b c$
$\text{D.}$ $\frac{c}{a}>\frac{b}{c}$
从某个月的月历表中取一个 $2 \times 2$ 方块. 已知这个方块所围成的 4 个方格的日期之和为 44 ,求这 4 个方格中的日期. 若设左上角的日期为x,则下列方程正确的是
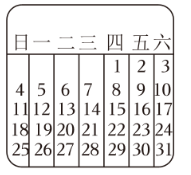
$\text{A.}$ $x+(x+1)+(x+7)+(x+14)=44$
$\text{B.}$ $x+(x+1)+(x+6)+(x+12)=44$
$\text{C.}$ $x+(x+1)+(x+7)+(x+8)=44$
$\text{D.}$ $x+(x+1)+(x+6)+(x+7)=44$
如图,在 $R t \triangle A B C$ 中, $\angle A C B=90^{\circ} , C D$ 为 $A B$ 边上的高线,设 $\angle A , \angle B , \angle A C B$ 所对的边分别为 $a , b , c$ ,则
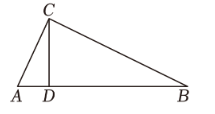
$\text{A.}$ $c=b \cos A+a \sin B$
$\text{B.}$ $c=b \sin A+a \sin B$
$\text{C.}$ $c=b \sin A+a \cos B$
$\text{D.}$ $c=b \cos A+a \cos B$
关于二次函数 $y=a(x-1)(x-3)+2(a < 0)$ 的下列说法中,正确的是
$\text{A.}$ 无论 $a$ 取范围内的何值,该二次函数的图象都经过 $(1,0)$ 和 $(3,0)$ 这两个定点
$\text{B.}$ 当 $x=2$ 时,该二次函数取到最小值
$\text{C.}$ 将该二次函数的图象向左平移 1 个单位,则当 $x < 0$ 或 $x>2$ 时, $y < 2$
$\text{D.}$ 设该二次函数与 $x$ 轴的两个交点的横坐标分别为 $m , n(m < n) ,$ 则 $1 < m < n < 3$
如图, $A B$ 是 $\odot O$ 的直径,弦 $C D \perp A B$ 于点 $E$ ,在 $B C$ 上取点 $F$ ,使得 $C F=C E$ ,连结 $A F$ 交 $C D$ 于点 $G$ ,连结 $A D$. 若 $C G=G F$ ,则 $\frac{B C^2}{A D^2}$ 的值等于

$\text{A.}$ $\frac{\sqrt{5}+1}{2}$
$\text{B.}$ $\frac{\sqrt{5}+3}{2}$
$\text{C.}$ $\frac{\sqrt{5}-1}{2}$
$\text{D.}$ $\frac{3-\sqrt{5}}{2}$
填空题 (共 4 题 ),请把答案直接填写在答题纸上
盒中有 $m$ 枚黑棋和 $n$ 枚白棋,这些棋除颜色外无其它差别. 从盒中随机取出一枚棋子,如果它是黑棋的概率是 $\frac{3}{5}$ ,则m关于n 的关系表达式为
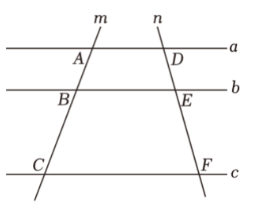
如图,直线m, $\mathrm{n}$ 被一组平行线 $\mathrm{a} , \mathrm{~b} , \mathrm{c}$ 所截. 若 $\frac{A B}{B C}=\frac{1}{2}$ ,则 $\frac{D E}{E F}=$
如图,在等腰 $Rt \triangle A B C$ 中, $\angle A C B=90^{\circ}$ ,若点 $E , F$ 分别在边 $A C$ 和边 $B C$ 上,沿直线 $E F$ 将 $\triangle C E F$ 翻折,使点 $C$ 落于 $\triangle A B C$ 所在平面内,记为点 $D$. 直线 $C D$ 交 $A B$ 于点 $G$.
(1)若 $\mathrm{CF}$ 落在边 $\mathrm{AB}$ 上,则 $\frac{A G}{G B}=$

(2) 若 $\frac{A G}{G B}=\lambda$ ,则 $\tan \angle \mathrm{CEF}=$ (用含的代数式表示).
解答题 (共 5 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
端午节是中国的传统节日,民间有端午节吃粽子的习俗,在端午节来临之际,某校七、八年级开展了一次 “包粽子" 实践活动,对学生的活动情况按 10 分制进行评分,成绩(单位: 分)均为不低于 6 的整数、为了解这次活动的效果,现从这两个年级各随机抽取10名学生的活动成绩作为样本进行活整理,并绘制统计图表,部分信息如表:
八年级 10 名学生活动成绩统计表

已知八年级 10 名学生活动成绩的中位数为 8.5 分.
请根据以上信息,完成下列问题:

七年级 10 名学生活动成绩扇形统计图
(1) 样本中,七年级活动成绩为7分的学生数是 $\qquad$ 七年级活动成绩的众数为 $\qquad$分;
(2) $a=$ $\qquad$ $b=$ $\qquad$
(3)若认定活动成绩不低于 9 分为 “优秀”,根据样本数据,判断本次活动中优秀率高的年级是否平均成绩也高,并说明理由.
如图,在 $\triangle A B C$ 中, $A B>A C$ , 点 $D$ 在 $A B$ 边上,点 $E$ 在 $A C$ 边上(点E不与 $A , C$ 重合),且 $\angle A E D=\angle B$.

(1) 求证: $\mathrm{AD} \cdot \mathrm{AB}=\mathrm{AE} \cdot \mathrm{AC}$.
(2) 若 $\mathrm{AE}=\mathrm{EC}=2 \mathrm{AD}$ ,求 $\frac{A D}{A B}$ 的值.
(3) 若 $A B=6, A C=4$ ,求 $A D$ 长的取值范围.
已知点 $A\left(m_1, n_1\right), B\left(m_2, n_2\right) \quad\left(m_1 < m_2\right)$ 在一次函数 $y=k x+b$ 的图象上.
(1) 用含有 $m_1 , n_1 , m_2 , n_2$ 的代数式表示 $k$ 的值.
(2) 若 $m_1+m_2=3 b , n_1+n_2=k b+4 , b>2$. 试比较 $n_1$ 和 $n_2$ 的大小,并说明理由.
如图,在正五边形 $A B C D E$ 中,连结 $A C, A D, C E, C E$ 交 $A D$ 于点F.
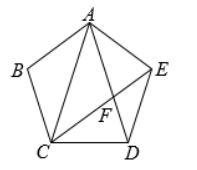
(1) 求 $\angle C A D$ 的度数.
(2) 已知 $A B=2$ ,求 $D F$ 的长.
如图,在矩形 $A B C D$ 中,点 $E , F$ 分别为对边 $A D , B C$ 的中点,线段 $E F$ 交 $A C$ 于点 $O$ ,延长 $C D$ 于点G,连结GE并延长交 $A C$于点 $Q$ , 连结 $G F$ 交 $A C$ 于点 $P$ , 连结 $Q F$.

(1) 若 $D G=\frac{1}{2} C D$.
①求证: 点 $Q$ 为 $O A$ 的中点.
② 若 $\mathrm{OA}=1 , \angle \mathrm{ACB}=30^{\circ}$ ,求 $\mathrm{QF}$ 的长.
(2) 求证: FE平分 $\angle Q F P$.
(3) 若 $\mathrm{CD}=\mathrm{mDG}$ ,求 $\frac{\mathrm{PF}}{\mathrm{QF}}$. (结果用含 $\mathrm{m}$ 的代数式表示).