解答题 (共 6 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
求最小的实数 $C>1$, 满足如下条件: 对任意整数 $n \geq 2$ 和满足 $\frac{1}{a_1}+$ $\frac{1}{a_2}+\cdots+\frac{1}{a_n}=1$ 的非整正实数 $a_1, a_2, \cdots, a_n$, 都可以找到正整数 $b_i$, 使得 (1)对 $1 \leq i \leq n, b_i=\left[a_i\right]$ 或 $\left[a_i\right]+1$ :
(2) $1 < \frac{1}{b_1}+\frac{1}{b_2}+\cdots+\frac{1}{b_n} \leq C$.
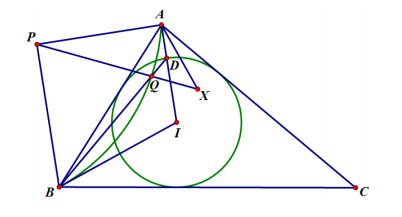
如图, $I$ 是 $\triangle A B C$ 的内心, 线段 $A I$ 交 $\triangle A B C$ 的内切圆于点 $D$, 已知 $B D \perp A C$. 设点 $P$ 满足 $\angle B P A=\angle P A I=90^{\circ}, Q$ 是线段 $B D$ 上一点, 使得 $\triangle A B Q$ 的外接圆与 $B I$ 相切. $X$ 是直线 $P Q$ 上一点, 使得 $\angle I A X=\angle X A C$,求证: $\angle A X P=45^{\circ}$.
设整数 $n>k \geq 1$, 质数 $p \mid \mathrm{C}_n^k$. 求证: 可以将 $\{1,2, \cdots, n\}$ 的所有 $k$ 元子集分成 $p$ 个类, 每类中的子集个数相同, 且元素和相等的两个子集属于同一类.
求所有的整数 $n \geq 2$, 使得平面上存在 $2 n$ 个不同点 $P_1, \cdots, P_n, Q_1, \cdots, Q_n$,满足:
(1) 这 $2 n$ 个点中任意三个不共线;
(2) 对任意 $1 \leq i \leq n, P_i P_{i+1} \geq 1$, 其中 $P_{n+1}=P_1$;
(3) 对任意 $1 \leq i \leq n, Q_i Q_{i+1} \geq 1$, 其中 $Q_{n+1}=Q_1$;
(4) 对任意 $1 \leq i, j \leq n, P_i Q_j \leq 1$.
设 $a_1 < a_2 < \cdots < a_{2024}$ 是正整数等差数列, $b_1 < b_2 < \cdots < b_{2024}$ 是正整数等比数列. 求同时出现在两个数列中的整数个数的最大可能值.
求所有的函数 $f: \mathbb{R} \rightarrow \mathbb{R}$, 使得对任意实数 $x, y$, 均有
$$
f(x f(y))+f(y)=f(x+y)+f(x y) .
$$