单选题 (共 10 题 ),每题只有一个选项正确
$-\frac{3}{5}$ 的倒数是
$\text{A.}$ $-\frac{3}{5}$
$\text{B.}$ $-\frac{5}{3}$
$\text{C.}$ $\frac{5}{3}$
$\text{D.}$ $\frac{3}{5}$
2021 年春节档电影 《你好, 李焕英》, 温馨、有趣, 体现了深厚的母女之情,收获好评的同时也成为了票房黑马. 截止 3 月 6 日 13: 43: 32, 《你好, 李焕英》票房成功突破 50 亿, 成为中国影史上第三部突破 50 亿票房大关的电影. 其中 50 亿用科学记数法表示为
$\text{A.}$ $50 \times 10^8$
$\text{B.}$ $5 \times 10^9$
$\text{C.}$ $5 \times 10^{10}$
$\text{D.}$ $0.5 \times 10^{10}$
下列四个图形中, 既是轴对称图形, 又是中心对称图形的是
$\text{A.}$  $\text{B.}$
$\text{B.}$  $\text{C.}$
$\text{C.}$  $\text{D.}$
$\text{D.}$ 
下列选项中, $\mathrm{y}$ 是 $\mathrm{x}$ 的反比例函数的是
$\text{A.}$ $y=\frac{3}{x^2}$
$\text{B.}$ $y=\frac{4 x}{5}$
$\text{C.}$ $y=-2 x^{-1}$
$\text{D.}$ $y=\frac{k}{x}$
下列调查中, 适合于采用普查方式的是
$\text{A.}$ 调查央视 “五一晚会” 的收视率
$\text{B.}$ 了解外地游客对兴城旅游景点的印象
$\text{C.}$ 了解一批新型节能灯的使用寿命
$\text{D.}$ 了解某航班上的乘客是否都持有 “绿色健康码”
下列四个命题: (1)直角三角形斜边上的中线等于斜边的一半; (2)对角线相等的平行四边形是菱形; (3)一组邻边相等的矩形是正方形; (4)三角形三条角平分线的交点是三角形的外心. 其中真命题共有
$\text{A.}$ 1个
$\text{B.}$ 2个
$\text{C.}$ 3个
$\text{D.}$ 4个
如图, $\angle \mathrm{AOB}=60^{\circ}$, 以点 $\mathrm{O}$ 为圆心, 以任意长为半径作弧交 $\mathrm{OA}, \mathrm{OB}$ 于 $\mathrm{C}$, $\mathbf{D}$ 两点; 分别以 $\mathbf{C}, \mathbf{D}$ 为圆心, 以大于 $\frac{1}{2} \mathbf{C D}$ 的长为半径作弧, 两弧相交于点 $\mathbf{P}$;以 $O$ 为端点作射线 $O P$, 在射线 $O P$ 上截取线段 $O M=6$, 则 $M$ 点到 $O B$ 的距离为

$\text{A.}$ 6
$\text{B.}$ 2
$\text{C.}$ 3
$\text{D.}$ 4
如图, $O A$ 为 $\odot O$ 的半径, 弦 $B C \perp O A$ 于点 $P$. 若 $B C=8, A P=2$, 则 $\odot O$ 的半径长为
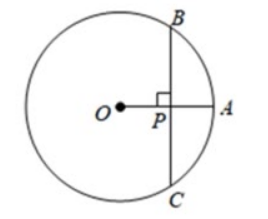
$\text{A.}$ 5
$\text{B.}$ 6
$\text{C.}$ 10
$\text{D.}$ 12
高铁为居民出行提供了便利, 从铁路沿线相距 $360 \mathrm{~km}$ 的甲地到乙地, 乘坐高铁列车比乘坐普通列车少用 $3 \mathrm{~h}$. 已知高铁列车的平均速度是普通列车平均速度的 3 倍, 设普通列车的平均速度为 $x \mathrm{~km} / \mathrm{h}$, 依题意, 下面所列方程正确的是
$\text{A.}$ $\frac{360}{x}-\frac{360}{3 x}=3$
$\text{B.}$ $\frac{360}{3 x}-\frac{360}{x}=3$
$\text{C.}$ $\frac{360}{x}-\frac{360}{\frac{1}{3} x}=3$
$\text{D.}$ $\frac{360}{\frac{1}{3} x}-\frac{360}{x}=3$
填空题 (共 6 题 ),请把答案直接填写在答题纸上
一个不透明的袋中装有 2 个红球和 4 个黄球, 这些球除颜色外完全相同. 从袋中随机摸出一个球, 摸到黄球的概率是
如图, 直线 $\boldsymbol{a}, \boldsymbol{b}$ 被直线 $\boldsymbol{c}$ 所截, 已知 $\boldsymbol{a} / / \boldsymbol{b}, \angle 1=130^{\circ}$, 则 $\angle 2$ ________ 为度.

已知关于 $x$ 的一元二次方程 $x^2-(2 k-1) x+k^2+3=0$ 有两个不相等的实数根, 则实数 $k$ 的取值范围是
用半径为 $3 \mathrm{~cm}$, 圆心角是 $120^{\circ}$ 的扇形围成一个圆锥的侧面, 则这个圆锥的底面半径等于 ________ cm.
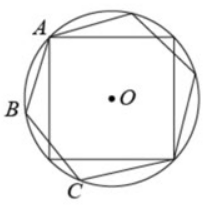
如图, $A B, A C$ 分别为 $\odot O$ 的内接正六边形, 内接正方形的一边, $B C$ 是圆内接 $\boldsymbol{n}$ 边形的一边,则 $\boldsymbol{n}$ 等于
解答题 (共 8 题 ),解答过程应写出必要的文字说明、证明过程或演算步骤
先化简, 再求值: $\frac{a+1}{a^2-2 a+1} \div\left(2+\frac{3-a}{a-1}\right)$, 其中 $\boldsymbol{a}=\sqrt{2}+1$.
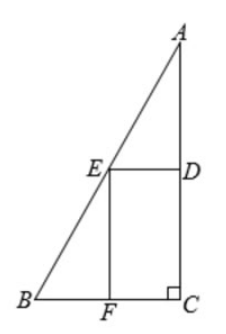
在 $R t \triangle A B C$ 中, $\angle C=90^{\circ}, D, E, F$ 分别是 $A C, A B, B C$ 的中点, 连接 $E D$, $E F$. 求证: 四边形 $D E F C$ 是矩形.
为提高学生的安全意识, 学校就学生对校园安全知识的了解程度, 对部分学生进行了问卷词查, 将收集信息进行统计分成 $A 、 B 、 C 、 D$ 四个等级, 其中 $\boldsymbol{A}$ :非常了解; $\boldsymbol{B}$ : 基本了解; $\boldsymbol{C}$ : 了解很少; $\boldsymbol{D}$ : 不了解. 并将结果绘制成如下两幅不完整的统计图. 请你根据统计信息解答下列问题.

(1) 接受问卷调查的学生共有
(2) 求扇形统计图中 “ $D$ ” 等级的扇形的图心角的度数, 并补全条形统计图;
(3) 七年一班从 “ $A$ ” 等级的 2 名女生和 2 名男生中随机抽取 2 人参加学校竞赛,请用列表或树状图的方法求出恰好抽到 1 名男生和 1 名女生的概率.
已知关于 $x$ 的一元二次方程 $x^2-6 x+(2 m+1)=0$ 有实数根.
(1) 求 $m$ 的取值范围;
(2) 如果方程的两个实数根为 $x_1, x_2$, 且 $2 x_1 x_2+x_1+x_2 \geq 20$, 求 $m$ 的取值范围.
如图, 在平面直角坐标系中, 直线 $y=2 x-2$ 与反比例函数 $y=\frac{k}{x}$ 的图象在第一象限交于点 $A(2, n)$, 在第三象限交于点 $B$, 过点 $B$ 作 $B C \perp x$ 轴于 $C$, 连接 $A C$.
(1) 求反比例函数的解析式;
(2) 求 $\triangle A B C$ 的面积;
(3) 根据图象直接写出不等式 $2 x-2 < \frac{k}{x}$ 的解集.

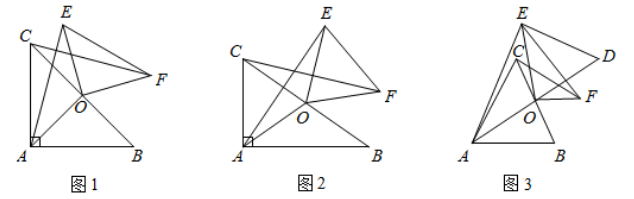
已知在 $\triangle A B C$ 中, $O$ 为 $B C$ 边的中点, 连接 $A O$, 将 $\triangle A O C$ 绕点 $O$ 顺时针方向旋转 (旋转角为钝角), 得到 $\triangle E O F$, 连接 $A E, C F$.
(1) 如图1, 当 $\angle B A C=90^{\circ}$ 且 $A B=A C$ 时, 则 $A E$ 与 $C F$ 满足的数量关系是
(2) 如图2, 当 $\angle B A C=90^{\circ}$ 且 $A B \neq A C$ 时, (1) 中的结论是否仍然成立? 若成立, 请写出证明过程; 若不成立, 请说明理由.
(3) 如图 3 , 延长 $A O$ 到点 $D$, 使 $O D=O A$, 连接 $D E$, 当 $A O=C F=5, B C=6$ 时, 求 $D E$ 的长.
阅读: $\triangle A B C$ 中, $a, b, c$ 分别是 $\angle A, \angle B, \angle C$ 的对边, $\triangle A B C$ 的边角有如下性质:
(1)正弦定理: $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$
(2)余弦定理: $a^2=b^2+c^2-2 b c \cos A, b^2=a^2+c^2-2 a c \cos B, c^2=a^2+b^2-2 a b \cos C$.
(3) $S_{\triangle A B C}=\frac{1}{2} a b \sin C=\frac{1}{2} b c \sin A=\frac{1}{2} a c \sin B$, 其中 $S_{\triangle A B C}$ 表示 $\triangle A B C$ 的面积.
请你根据上述结论求解下列问题:
(1) 在锐角 $\triangle A B C$ 中, $a, b, c$ 分别是 $\angle A, \angle B, \angle C$ 的对边, 若 $b=3, a+c=4,2 b \sin A=\sqrt{3} a$. 求 $\angle B$ 的大小及 $\triangle A B C$ 的面积;
(2) 在四边形 $A B C D$ 中, $A B=7, A C=6, \cos \angle B A C=\frac{11}{14}, C D=6 \sin \angle D A C$, 求 $B D$ 的最大值.
已知抛物线 $y=x^2+b x+c$ 经过点 $B$, 与 $y$ 轴交于点 $A$, 顶点 $P$ 在直线 $O B$ 上.
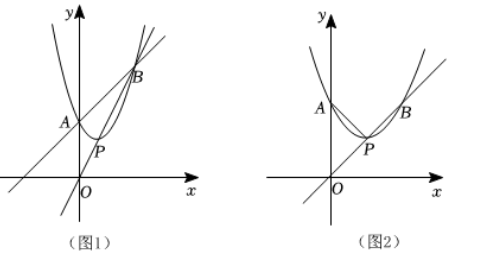
(1) 如图1, 若点 $B$ 的坐标为 $(3,6)$, 点 $P$ 的横坐标为 1 .
(1)试确定抛物线的解析式;
(2)若当 $m \leq x \leq 4$ 时, $y=x^2+b x+c$ 的最小值为 2 , 最大值为 11 , 请求出 $m$ 的取值范围;
(3)已知: 点 $M$ 在抛物线上, 点 $N$ 的坐标为 $(2,3)$, 且 $\angle M N A=\angle B A N$, 请直接写出符合题意的点 $M$ 的坐标.
(2) 如图 2 , 若点 $P$ 在第一象限, 且 $P A=P O$, 过点 $P$ 作 $P D \perp x$ 轴于 $D$, 将抛物线 $y=x^2+b x+c$ 平移, 平移后的抛物线经过点 $A 、 D$,与 $x$ 轴的另一个交点为 $C$, 试探究四边形 $O A B C$ 的形状, 并说明理由.