单选题 （共 8 题 ），每题只有一个选项正确
若复数 $z=1-\mathrm{i}$ 的共轭复数为 $\bar{z}$ ，则 $\frac{2}{z}+\bar{z}=$
$\text{A.}$ 2－2i
$\text{B.}$ $2+2 \mathrm{i}$
$\text{C.}$ $-1+\mathrm{i}$
$\text{D.}$ $3-\mathrm{i}$
已知集合 $S=\left\{s \left\lvert\, s=\frac{2 \pi}{5} n+\frac{\pi}{3}\right., n \in \mathrm{Z}\right\}, T=\left\{t \left\lvert\, t=\frac{2 \pi}{15} n+\frac{\pi}{5}\right., n \in \mathrm{Z}\right\}$ ，则 $S \cup T$
$\text{A.}$ $\varnothing$
$\text{B.}$ s
$\text{C.}$ $T$
$\text{D.}$ $Z$
在四棱锥 $P-A B C D$ 中，$P A \perp$ 底面 $A B C D$ ，且 $A B C D$ 为正方形，则此四棱锥表面中互相垂直的面有
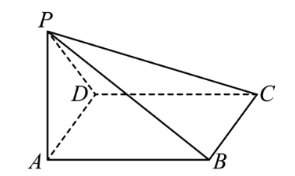
$\text{A.}$ 6 对
$\text{B.}$ 5 对
$\text{C.}$ 4 对
$\text{D.}$ 3 对
甲、乙两名同学参加了班级组织的数学知识有奖竞答活动，二人从各自的 10 道题中（这 20 道题均不相同）各自独立地随机抽取 2 道题现场回答，已知在每人的 10 道题中，均有 5 道是代数题 ， 5 道是几何题，则甲、乙两名同学抽取的 4 道题目中有且仅有 2 道代数题的概率为
$\text{A.}$ $\frac{25}{81}$
$\text{B.}$ $\frac{1}{2}$
$\text{C.}$ $\frac{11}{27}$
$\text{D.}$ $\frac{3}{4}$
已知一个正方体内接于一个球，过球心作一截面，则截面不可能是
$\text{A.}$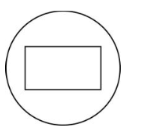 
$\text{B.}$ 
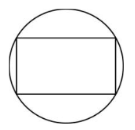$\text{C.}$ 
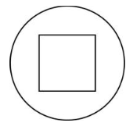$\text{D.}$ 
《九章算术•商功》中将正四面形棱台（即正四棱台）建筑物称为方亭．现有一方亭 $A B C D- A_1 B_1 C_1 D_1$ ，已知 $A B=1$ ，且该方亭的高为 6 ，体积为 26 ，则 $A_1 B_1=$
$\text{A.}$ 2
$\text{B.}$ 3
$\text{C.}$ 4
$\text{D.}$ 5
在 $\triangle A B C$ 中，角 $A, B, C$ 所对应的边分别为 $a, b, c$ ．若 $\sin B+2 \sin C \cos A=0$ ，则角 $B$ 的最大值为
$\text{A.}$ $\frac{\pi}{6}$
$\text{B.}$ $\frac{\pi}{4}$
$\text{C.}$ $\frac{\pi}{3}$
$\text{D.}$ $\frac{2 \pi}{3}$
8．已知 $\sin \left(\alpha-\frac{\pi}{4}\right)=\frac{\sqrt{3}}{2}$ ，则 $\cos \left(\frac{2005 \pi}{2}-2 \alpha\right)=$
$\text{A.}$ $\frac{1}{2}$
$\text{B.}$ $-\frac{\sqrt{3}}{2}$
$\text{C.}$ $-\frac{1}{2}$
$\text{D.}$ $\frac{\sqrt{3}}{2}$
多选题 （共 3 题 ），每题有多个选项正确
降雨量是指从天空降落到地面上的雨水，未经蒸发、渗透、流失，而在水平面上积聚的水层深度，一般以毫米为单位．降雨量可以直观地反映一个地区某一时间段内降水的多少，它对农业生产、水利工程、城市排水等有着重要的影响．如图，这是 $A, B$ 两地某年上半年每月降雨量的折线统计图．下列结论正确的是
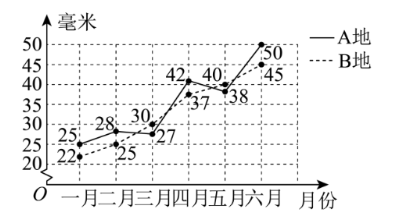
$\text{A.}$ 这年上半年 $A$ 地月平均降雨量比 $B$ 地月平均降雨量大
$\text{B.}$ 这年上半年 $A$ 地月降雨量的中位数比 $B$ 地月降雨量的中位数大
$\text{C.}$ 这年上半年 $A$ 地月降雨量的极差比 $B$ 地月降雨量的极差大
$\text{D.}$ 这年上半年 $A$ 地月降雨量的 $80 \%$ 分位数比 $B$ 地月平均降雨量的 $80 \%$ 分位数大
已知正方体 $A B C D-A_1 B_1 C_1 D_1$ 的棱长为 1 ，点 $M$ 为线段 $C C_1$（含端点）上的动点，由点 $\mathrm{A}, D_1$ ，$M$ 确定的平面为 $\alpha$ ，则下列说法正确的是
$\text{A.}$ 平面 $\alpha$ 截正方体的截面可能为等腰梯形
$\text{B.}$ 平面 $\alpha$ 截正方体的截面可能为菱形
$\text{C.}$ 点 $M$ 运动过程中，三棱锥 $A_1-A D_1 M$ 的体积为定值
$\text{D.}$ 三棱锥 $A_1-A D_1 M$ 的外接球表面积的最小值为 $\frac{41}{16} \pi$
连续抛掷一枚硬币两次，事件 $A$ 表示＂第一次硬币正面朝上＂，事件 $B$ 表示＂第二次硬币反面朝上＂，事件 $C$ 表示＂两次硬币都正面朝上＂，事件 $D$ 表示＂两次硬币朝上的情况不同＂，则
$\text{A.}$ $A$ 与 $C$ 相互独立
$\text{B.}$ $A$ 与 $D$ 相互独立
$\text{C.}$ $B$ 与 $C$ 相互独立
$\text{D.}$ $B$ 与 $D$ 相互独立
填空题 （共 3 题 ），请把答案直接填写在答题纸上
已知圆台形的花盆的上、下底面的直径分别为 4 和 8 ，该花盆的侧面展开图的扇环所对的圆心角为 $\frac{\pi}{2}$ ，则该圆台的母线长为
写出圆 $C_1:(x-1)^2+y^2=1$ 与圆 $C_2:(x-4)^2+(y-4)^2=16$ 的一条公切线的方程
如图，茂名的城市雕像＂希望之泉＂是茂名人为了实现四个现代化而努力奋斗的真实写照．被托举的四个球堆砌两层放在平台上，下层 3 个，上层 1 个，两两相切．若球的半径都为 $a$ ，则上层的最高点离平台的距离为
解答题 （共 5 题 ），解答过程应写出必要的文字说明、证明过程或演算步骤
为加深学生对新中国成立以来我国在经济建设、科技创新、精神文明建设等方面取得成就的了解，某学校高二年级组织举办了知识竞赛。选拔赛阶段采用逐一答题的方式，每位选手最多有 5 次答题机会，累计答对 3 道题则进入初赛，累计答错 3 道题则被淘汰．初赛阶段参赛者每两人一组进行比赛，组织者随机从准备好的题目中抽取 2 道试题供两位选手抢答，每位选手抢到每道试题的机会相等，得分规则如下：选手抢到试题且回答正确得 10 分，对方选手得 0 分，选手抢到试题但没有回答正确得 0 分，对方选手得 5 分， 2 道试题抢答完毕后得分少者被淘汰，得分多者进入决赛（若分数相同，则同时进入决赛）．
（1）已知选拔赛中选手甲答对每道试题的概率为 $\frac{2}{3}$ ，且回答每道试题是否正确相互独立，求甲进入初赛的概率；
（2）已知初赛中选手甲答对每道试题的概率为 $\frac{4}{5}$ ，对手答对每道试题的概率为 $\frac{3}{4}$ ，两名选手回答每道试题是否正确相互独立，求初赛中甲的得分 $Y$ 的分布列与期望；
（3）进入决赛后，每位选手回答 4 道试题，至少答对 3 道试题胜出，否则被淘汰，已知选手甲进入决赛，且决赛中前 3 道试题每道试题被答对的概率都为 $(p \in(0,1))$ ，若甲 4 道试题全对的概率为 $\frac{1}{16}$ ，求甲能胜出的概率的最小值．
如图，四棱锥 $P-A B C D$ 中，$P A=P D=A D=C D=2$ ，底面 $A B C D$ 是个直角梯形，$A D / / B C$ ，$\angle D A B=90^{\circ}, \angle A D C=60^{\circ}$ ．
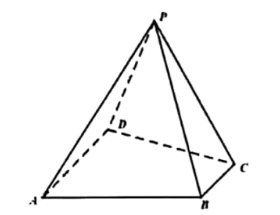
（1）证明：$P C \perp A D$ ；
（2）若二面角 $P-A D-B$ 的大小为 $60^{\circ}$ ，在棱 $P B$ 上是否存在点 $G$（不与端点重合），使得直线$C G$ 与平面 $P A D$ 所成的角的正弦值为 $\frac{\sqrt{21}}{7}$ ？若存在，求 $\frac{P G}{P B}$ 的值，若不存在，说明理由．
设 $n(n \geq 2)$ 为正整数，集合 $U=\{1,2,3, \cdots, n\}$ ，集合 $A=\left\{t_1, t_2, \cdots, t_m\right\}\left(m \in \mathbf{N}^*, m \leq n\right)$ 为 $U$ 的一个非空子集，记 $S(A)=q^{t_1}+q^{t_2}+\cdots+q^{t_m}$ ，其中 $q \geq 2$ 。
（1）若 $n=2, q=3$ ，求 $S(A)$ 的取值的集合；
（2）证明：$S(A)$ 的所有可能取值个数为 $2^n-1$ ；
（3）是否存在 $q$ ，使得 $S(A)$ 的所有可能取值从小到大排列成等差数列，若存在，求 $q$ ；若不存在 ，说明理由．
欧拉公式 $\mathrm{e}^{\mathrm{i} x}=\cos x+\mathrm{i} \sin x(x \in \mathrm{R}), \mathrm{e}$ 是自然对数的底， i 是虚数单位．它的一个简单而重要的结论是：余弦函数和正弦函数可以用定义在复数集上的指数函数构造出来，即 $\cos x= \frac{\mathrm{e}^{\mathrm{i} x}+\mathrm{e}^{\mathrm{i} x}}{2}, \sin x=\frac{\mathrm{e}^{\mathrm{i} x}-\mathrm{e}^{-\mathrm{i} x}}{2 \mathrm{i}}(x \in \mathrm{R})$ 。欧拉公式将指数函数的定义域扩大到复数集，建立了三角函数和指数函数的关系，被誉为＂数学中的天桥＂．当 $x=\pi$ 时，得到等式 $\mathrm{e}^{\mathrm{i} \pi}+1=0$ ，数学里最重要的五个常数 $\mathrm{e}, \pi, \mathrm{i}, 1,0$ 被联系在一起，仿佛一句诗，道尽了数学之美．
（1）证明：若 $x \in \mathrm{R}$ ，则 $\mathrm{e}^{\mathrm{i} x}$ 与 $\mathrm{e}^{-\mathrm{i} x}$ 互为共轭复数；
（2）已知 $\mathrm{e}^{z_1} \mathrm{e}^{z_2}=\mathrm{e}^{z_1+z_2}\left(z_1, z_2 \in \mathrm{C}\right)$ ，欧拉公式在复数集内可推广为 $\mathrm{e}^{\mathrm{i} z}=\cos z+\mathrm{i} \sin z, \mathrm{e}^{-\mathrm{i} z}= \cos z-\mathrm{i} \sin z(z \in \mathrm{C})$ ，需要指出的是， $\cos z$ 和 $\sin z$ 是复数，它们不是 $\mathrm{e}^{\mathrm{i} z}$ 的实部和虚部，且 $\cos z=\frac{\mathrm{e}^{\mathrm{i} z}+\mathrm{e}^{-\mathrm{i} z}}{2}, \sin z=\frac{\mathrm{e}^{\mathrm{i} z}-\mathrm{e}^{-\mathrm{i} z}}{2 \mathrm{i}}(z \in \mathrm{C})$ 。容易证明，两角和的余弦公式在复数范围内仍然成立，即 $\cos \left(z_1+z_2\right)=\cos z_1 \cos z_2-\sin z_1 \sin z_2\left(z_1, z_2 \in \mathrm{C}\right)$ 。定义函数 $\cosh z=\cos (\mathrm{i} z), \quad \sinh z=-\mathrm{i} \sin (\mathrm{i} z)(z \in \mathrm{C})$ ．证明： $\cosh \left(z_1+z_2\right)=\cosh z_1 \cosh z_2+\sinh z_1 \sinh z_2\left(z_1, z_2 \in \mathrm{C}\right)$ ；
（3）若 $a, x, y \in \mathrm{R}$ ，令 $z=a+\mathrm{i} \ln 2, \cos z=x+y \mathrm{i}$ ，证明：$\frac{16 x^2}{25}+\frac{16 y^2}{9}=1$ ．
已知函数 $f(x)=\frac{\ln x+a}{x}-\frac{a}{2}(a \in \mathbf{R})$ ．
（1）当 $a=1$ 时，求曲线 $f(x)$ 切线斜率的最小值；
（2）若 $g(x)=x^2 f(x)$ 有两个不同的极值点 $X_1, x_2$ ．
（i）求 $a$ 的取值范围；
（ii）求证：$x_1 x_2>\mathrm{e}^{-2 a}$ ．